Комбінація циліндра і призми. Приклади задач

Комбінація циліндра і призми. Приклади задач 

№1. Основою прямої призми є рівнобедрений трикутник з кутом β при вершині. Діагональ бічної грані, що містить основу цього трикутника, дорівнює 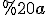 і нахилена до площини основи під кутом 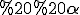. Визначити повну поверхню циліндра, описаного навколо призми.

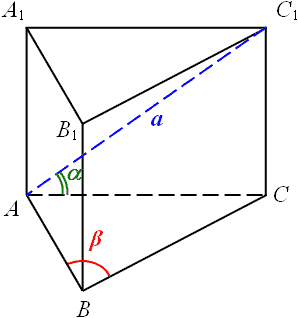Зауваження: Для розв'язання задачі достатньо розглянути малюнок призми, оскільки висота циліндра співпадає з висотою призми (пряма). Описувати коло (див. означення) навколо основи призми немає необхідності.

Розв'язання.

Нехай Δ ABC - рівнобедрений, з кутом 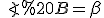 при вершині. Діагональ бічної грані, що містить основу трикутника AC₁=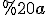, кут нахилу відрізка АС₁ до площини основи .

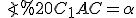Оскільки призма пряма, будемо вважати відрізок СС₁ висотою призми і циліндра: H=CC^₁.

З 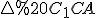:  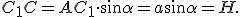    (1)

Скористаємося формулою 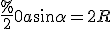 для обчислення радіуса основи циліндра.

Запишемо 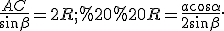   (2)

Повна поверхня циліндра . Підставивши значення рівностей (1) та (2), маємо:

Відповідь: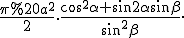 

№2. Основа прямої призми - ромб зі стороною 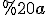 і кутом 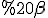, який утворює ця сторона з більшою діагоналлю ромба. Менша діагональ призми утворює з площиною основи кут 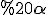. Визначити об'єм циліндра, вписаного в цю призму.

Розв'язання.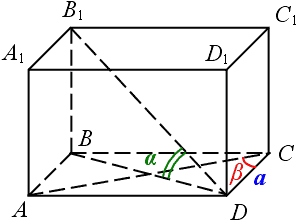

Розглянемо основу прямої призми ABCDA₁B₁C₁D₁. В основі ромб ABCD, нехай AC - більша, а BD - менша його діагоналі. Тоді  - кут між меншою діагоналлю призми і площиною основи.
Покладемо , де  - висота призми і циліндра.

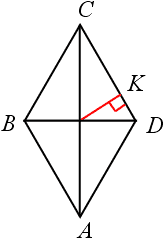Розглянемо трикутник : в ньому , тоді .

З   маємо:
. (1)
Оскільки циліндр вписаний в призму, то круг, що знаходиться в основі циліндра, вписано в ромб. Розглянемо малюнок.
В ромбі  відрізок  є радіусом вписаного кола в ромб. Бачимо, що для знаходження можна розглянути , в якому знайдено раніше відрізок , а . Отже, .
 (2) (Зауваження ).
Обчислимо об'єм циліндра, підставляючи значення з рівності (1) та (2):
.


Відповідь: .