РОЗВ’ЯЗУВАННЯ ЗАДАЧ НА ПОБУДОВУ ПЕРЕРІЗІВ
ЗАДАЧА 1. Точка М лежить на бічній грані ADB тетраедра DABC (мал. 1). Побудуйте переріз тетраедра площиною, яка проходить черві точку Мпаралельно основі ABC.

Мал. 1
Розв'язання
Оскільки січна площина паралельна площині ABC, то вона паралельна прямим АВ, ВС і СА. Отже, січна площина перетинає бічні грані тетраедра по прямих, паралельних сторонам трикутника ABC. Проведемо через точку М пряму, паралельну АВ, і позначимо буквами К і Р точки перетину цієї прямої з ребрами DB і DA відповідно. Потім через точку Р проведемо пряму, паралельну АС, позначимо буквою L точку перетину цієї прямої з ребромDC. Отже, трикутник LKP — шуканий переріз.
ЗАДАЧА 2. На ребрах паралелепіпеда дано три точки А, В і С. Побудуйте переріз паралелепіпеда площиною ABC.
Розв'язання
Побудова шуканого перетину залежить від того, на яких ребрах паралелепіпеда лежать точки А, В і С. Розглянемо три випадки.
Проводимо відрізки АВ, ВС і АС і одержуємо шуканий переріз — трикутник ABC (мал. 2, а).
Через точку ^ проведемо пряму, паралельну прямій ВС. Це і є пряма, по якій січна площина перетинається із площиною нижньої основи; вона перетинає ребра нижньої основи в точках Е і F. Потім через точку Е проведемо пряму, паралельну прямій АВ, і одержимо точку D. Нарешті, проводимо відрізки AF і CD і одержуємо шуканий переріз — шестикутник ABCDEF (мал. 2, в).

Мал. 2
ЗАДАЧА 3. Побудуйте переріз куба ABCDAlB1C1D1 площиною, яка проходить через точки С1 , С і К, де К — середина AlB1. З'ясуйте, яка фігура утвориться в перерізі.
Розв'язання

Мал. 3
Пряма С1К належить січній площині (мал. 3) (точки С1 і К лежать у площині AlB1C1 . Проведемо пряму КМ, паралельну прямій CC1 (KM також лежить у січній площині).
Проведемо в площині ABC пряму СМ, паралельну прямій KC1 (січна площина перетинає площину ABC по прямій, паралельній КС1, оскільки (AlB1C1) || (ABC) як площини протилежних граней куба).
ЗАДАЧА 4. Точка Р ділить ребро АВ куба ABCDAlB1C1D1 у відношенні АР: РВ = 1:3. Побудуйте переріз цього куба площиною, яка паралельна площині AlC1А і проходить через точку Р. Ребро куба дорівнює 4 см. Знайдіть периметр перерізу.
Розв'язання
Проведемо пряму FK, паралельну прямій АС (мал. 4). Точка К ділить відрізок ВС у відношенні 3:1, рахуючи від вершини В (узагальнена теорема Фалеса). Проведемо пряму FP1, паралельну прямій AA1. Тоді площини AlC1А і F1FK паралельні (за ознакою паралельності площин).
Пряма F1K1 паралельна прямій AlC1 за властивістю паралельних площин.
Чотирикутник FF1К1К — паралелограм, більше того, прямокутник, оскільки АА1 ∥ АВ, отже, FF1 ⊥ FК.
 FF1 = А1А = 4.
FF1 = А1А = 4.
Щоб знайти РК, розглянемо трикутники АСВ і FКВ. Вони
подібні за двома пропорційними сторонами і куту між ними.
 , оскільки АС = 4
, оскільки АС = 4  (діагональ квадрата АВСВ).
(діагональ квадрата АВСВ).

 (см)
(см)
Тоді (см2)
(см2)

 (см)
(см)
Мал. 4
Відповідь : см;
см;  см2
см2
ЗАДАЧА 5. У тетраедрі DABC точка М належить ребру BD. Подуйте переріз тетраедра площиною, яка проходить через точу М паралельно ребрам ADі ВС. Визначте вид перерізу.
Розв'язання
Проведемо в грані ABD пряму MS, паралельну ребру АО, а в грані ABC — пряму SP, паралельну ребру ВС (мал. 5). Через прямі MS і SP, що перетинаються, проведемо площину, яка перетне грань ADC по прямій PN, а грань BCD — по прямій MN. Оскільки ребра AD і ВС не лежать у площині MSP і паралельні прямим MS і SP цієї площини, то прямі AD і ВС паралельні площині MSP (ознака паралельності
прямої та площини)
Мал. 5
Оскільки площина BCD проходить через пряму ВС, паралельну площині MSP, і перетинає її по прямій MN, то MN ∥ BC. Якщо MN ∥ BC, a BC ∥ SP,то MN ∥ SP. Аналогічно можна показати, що MS ∥ NP. Тоді шуканий переріз — паралелограм MSPN.
ЗАДАЧА 6. Побудувати переріз правильної чотирикутної призми
ABCDA1B1C1D1 площиною, яка проходить через точку М на бічному ребрі BB1 призми, паралельно діагоналі основи AC і мимобіжній із нею діагоналі призми BD1.
Розв'язання
Опираючись на твердження: якщо площина проходить через пряму, паралельну іншій площині, і перетинає цю площину, то лінія перетину площин паралельна даній прямій,— будуємо на мал. 6. MR — лінію перетину січної площини із площиною BB1D1. MR || BD1 (R — спільна точка січної площини і площини верхньої грані призми). Далі через точку Q перетину січної площини з віссю ОО1, призми проводимо в її діагональному перерізіAA1C1 C відрізок KN, паралельний діагоналі АС. Нарешті через точку R проводимо відрізок LP, паралельний відрізку KN,— лінію перетину січної площини з площиною верхньої основи призми.
Залишається послідовно сполучити відрізками точки М, N, Р, L, К, М.

Мал. 6 Мал. 7
ЗАДАЧА 7. Побудувати переріз правильної чотирикутної піраміди SABCD площиною, яка проходить через середину М сторони ВС основи паралельно діагоналі АС основи і бічному ребру SB.
Розв'язання
Будуємо лінії перетину січної площини із площинами ABC, DSB і ASC (мал. 7). Ці побудови дають нам всі шукані вершини перерізу:
а) MN ∥ АС, F — точка перетину відрізків MN і BD;
б) FL ∥ SB, Q — точка перетину відрізків SO і FL;
в) через точку Q будуємо відрізок КР так, що КР ∥ АL. Сполучаємо послідовно точки М, N, К, L і Р.
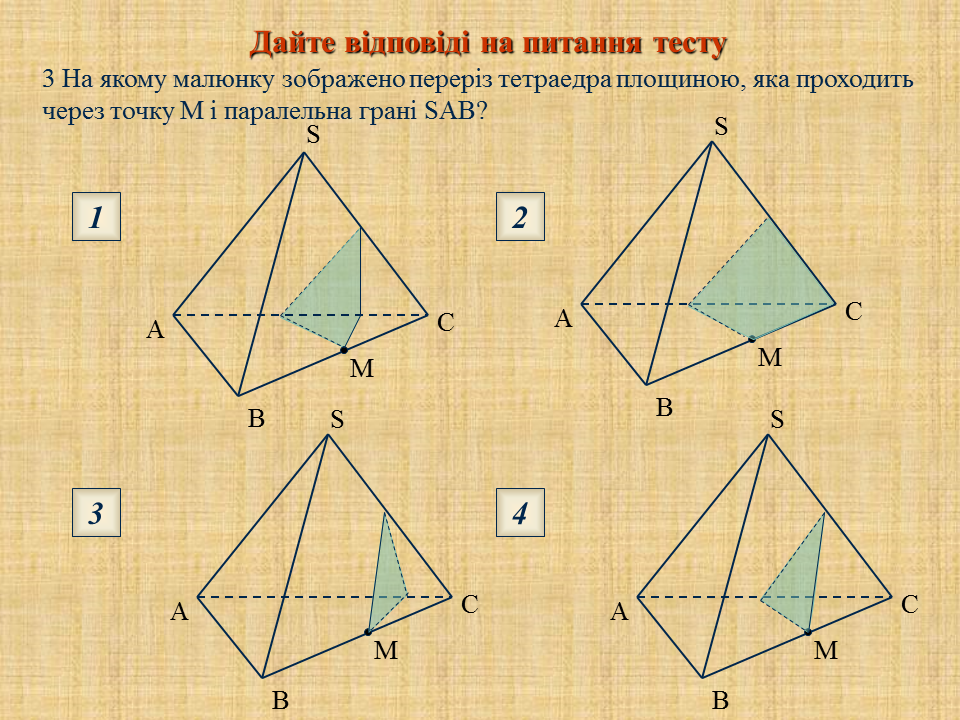
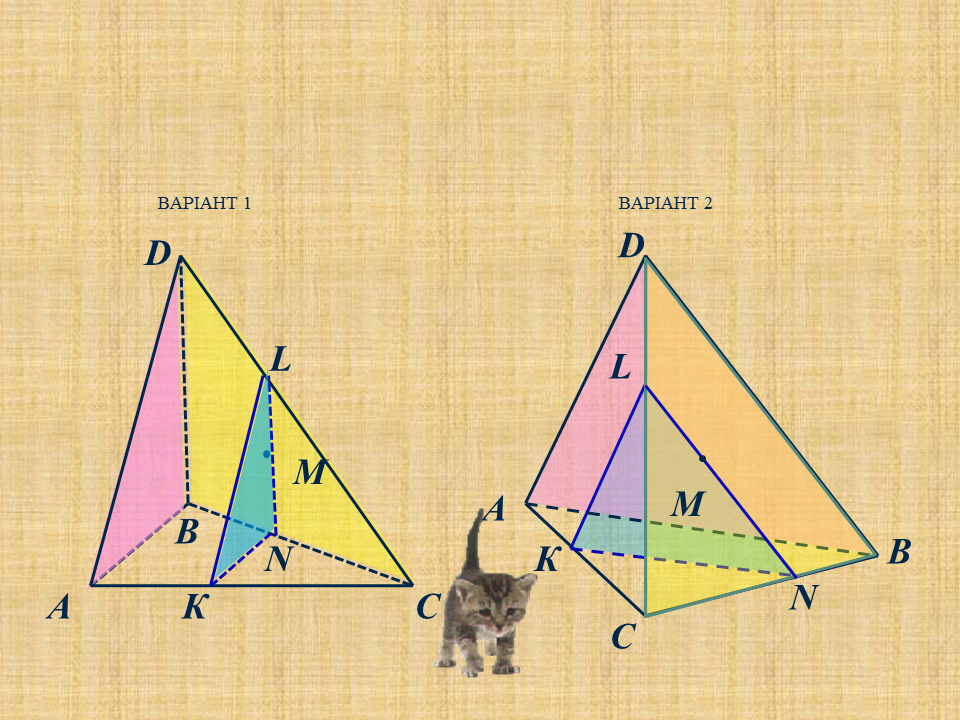
ЗАДАЧА 8. Побудувати переріз тетраедра площиною, яка проходить через центр основи паралельно бічній грані піраміди.
Розв'язання
Нехай січна площина паралельна грані АSВ піраміди ^ (мал. 8). Проводимо через центр О основи піраміди пряму МN паралельно АВ; сліди січної площини і бічних граней можна побудувати так: провести NК ∥ SВ і МК ∥ АS (прямі МК і NК перетинаються в точці К на ребрі SС).

Мал. 8
Розв’язати задачі:

ЗАДАЧА 1. Точка М лежить на бічній грані ADB тетраедра DABC (мал. 1). Побудуйте переріз тетраедра площиною, яка проходить черві точку Мпаралельно основі ABC.

Мал. 1
Розв'язання
Оскільки січна площина паралельна площині ABC, то вона паралельна прямим АВ, ВС і СА. Отже, січна площина перетинає бічні грані тетраедра по прямих, паралельних сторонам трикутника ABC. Проведемо через точку М пряму, паралельну АВ, і позначимо буквами К і Р точки перетину цієї прямої з ребрами DB і DA відповідно. Потім через точку Р проведемо пряму, паралельну АС, позначимо буквою L точку перетину цієї прямої з ребромDC. Отже, трикутник LKP — шуканий переріз.
ЗАДАЧА 2. На ребрах паралелепіпеда дано три точки А, В і С. Побудуйте переріз паралелепіпеда площиною ABC.
Розв'язання
Побудова шуканого перетину залежить від того, на яких ребрах паралелепіпеда лежать точки А, В і С. Розглянемо три випадки.
Точки лежать на ребрах, що виходять з однієї вершини (мал. 2, а).
Проводимо відрізки АВ, ВС і АС і одержуємо шуканий переріз — трикутник ABC (мал. 2, а).
Розміщення точок показано на мал. 2, б. Проводимо відрізки АВ і ВС, а потім через точку А проводимо пряму, паралельну ВС, а через точку С — пряму, паралельну АВ. Перерізом цих прямих з ребрами нижньої грані є точки Е і D. Залишається провести відрізок ED, і одержуємо шуканий переріз — п'ятикутник ABCDE (мал. 2, б).
Розміщення точок А, В і С показано на мал. 2, в. Спочатку побудуємо пряму, по якій січна площина перетинається з площиною нижньої основи. Для цього проведемо пряму АВ і продовжимо нижнє ребро, яке лежить у тій самій грані, що й пряма АВ, до перетину із цією прямою в точці М.
Через точку ^ проведемо пряму, паралельну прямій ВС. Це і є пряма, по якій січна площина перетинається із площиною нижньої основи; вона перетинає ребра нижньої основи в точках Е і F. Потім через точку Е проведемо пряму, паралельну прямій АВ, і одержимо точку D. Нарешті, проводимо відрізки AF і CD і одержуємо шуканий переріз — шестикутник ABCDEF (мал. 2, в).

Мал. 2
ЗАДАЧА 3. Побудуйте переріз куба ABCDAlB1C1D1 площиною, яка проходить через точки С1 , С і К, де К — середина AlB1. З'ясуйте, яка фігура утвориться в перерізі.
Розв'язання

Мал. 3
Пряма С1К належить січній площині (мал. 3) (точки С1 і К лежать у площині AlB1C1 . Проведемо пряму КМ, паралельну прямій CC1 (KM також лежить у січній площині).
Проведемо в площині ABC пряму СМ, паралельну прямій KC1 (січна площина перетинає площину ABC по прямій, паралельній КС1, оскільки (AlB1C1) || (ABC) як площини протилежних граней куба).
ЗАДАЧА 4. Точка Р ділить ребро АВ куба ABCDAlB1C1D1 у відношенні АР: РВ = 1:3. Побудуйте переріз цього куба площиною, яка паралельна площині AlC1А і проходить через точку Р. Ребро куба дорівнює 4 см. Знайдіть периметр перерізу.
Розв'язання
Проведемо пряму FK, паралельну прямій АС (мал. 4). Точка К ділить відрізок ВС у відношенні 3:1, рахуючи від вершини В (узагальнена теорема Фалеса). Проведемо пряму FP1, паралельну прямій AA1. Тоді площини AlC1А і F1FK паралельні (за ознакою паралельності площин).
Пряма F1K1 паралельна прямій AlC1 за властивістю паралельних площин.
Чотирикутник FF1К1К — паралелограм, більше того, прямокутник, оскільки АА1 ∥ АВ, отже, FF1 ⊥ FК.
Щоб знайти РК, розглянемо трикутники АСВ і FКВ. Вони
подібні за двома пропорційними сторонами і куту між ними.
Тоді

Мал. 4
Відповідь :
ЗАДАЧА 5. У тетраедрі DABC точка М належить ребру BD. Подуйте переріз тетраедра площиною, яка проходить через точу М паралельно ребрам ADі ВС. Визначте вид перерізу.
Розв'язання
Проведемо в грані ABD пряму MS, паралельну ребру АО, а в грані ABC — пряму SP, паралельну ребру ВС (мал. 5). Через прямі MS і SP, що перетинаються, проведемо площину, яка перетне грань ADC по прямій PN, а грань BCD — по прямій MN. Оскільки ребра AD і ВС не лежать у площині MSP і паралельні прямим MS і SP цієї площини, то прямі AD і ВС паралельні площині MSP (ознака паралельності

прямої та площини)
Мал. 5
Оскільки площина BCD проходить через пряму ВС, паралельну площині MSP, і перетинає її по прямій MN, то MN ∥ BC. Якщо MN ∥ BC, a BC ∥ SP,то MN ∥ SP. Аналогічно можна показати, що MS ∥ NP. Тоді шуканий переріз — паралелограм MSPN.
ЗАДАЧА 6. Побудувати переріз правильної чотирикутної призми
ABCDA1B1C1D1 площиною, яка проходить через точку М на бічному ребрі BB1 призми, паралельно діагоналі основи AC і мимобіжній із нею діагоналі призми BD1.
Розв'язання
Опираючись на твердження: якщо площина проходить через пряму, паралельну іншій площині, і перетинає цю площину, то лінія перетину площин паралельна даній прямій,— будуємо на мал. 6. MR — лінію перетину січної площини із площиною BB1D1. MR || BD1 (R — спільна точка січної площини і площини верхньої грані призми). Далі через точку Q перетину січної площини з віссю ОО1, призми проводимо в її діагональному перерізіAA1C1 C відрізок KN, паралельний діагоналі АС. Нарешті через точку R проводимо відрізок LP, паралельний відрізку KN,— лінію перетину січної площини з площиною верхньої основи призми.
Залишається послідовно сполучити відрізками точки М, N, Р, L, К, М.

Мал. 6 Мал. 7
ЗАДАЧА 7. Побудувати переріз правильної чотирикутної піраміди SABCD площиною, яка проходить через середину М сторони ВС основи паралельно діагоналі АС основи і бічному ребру SB.
Розв'язання
Будуємо лінії перетину січної площини із площинами ABC, DSB і ASC (мал. 7). Ці побудови дають нам всі шукані вершини перерізу:
а) MN ∥ АС, F — точка перетину відрізків MN і BD;
б) FL ∥ SB, Q — точка перетину відрізків SO і FL;
в) через точку Q будуємо відрізок КР так, що КР ∥ АL. Сполучаємо послідовно точки М, N, К, L і Р.
ЗАДАЧА 8. Побудувати переріз тетраедра площиною, яка проходить через центр основи паралельно бічній грані піраміди.
Розв'язання
Нехай січна площина паралельна грані АSВ піраміди ^ (мал. 8). Проводимо через центр О основи піраміди пряму МN паралельно АВ; сліди січної площини і бічних граней можна побудувати так: провести NК ∥ SВ і МК ∥ АS (прямі МК і NК перетинаються в точці К на ребрі SС).

Мал. 8
Розв’язати задачі:
Побудуйте переріз куба площиною, що задана прямою а і точкою М, яка належить одному з бічних ребер, за умови, що пряма а лежить у площині нижньої грані, але її не перетинає. Крім того, ця пряма не паралельна жодному з ребер нижньої грані, якщо точка М ділить ребро у відношенні 1:3, рахуючи від нижньої грані.
Побудуйте переріз тетраедра ABCD площиною, яка проходить через ребро DC і точку перетину медіан грані ABC.
Побудуйте перерізи многогранника площиною, яка проходить через точки М, N, Р (мал. 159, 160).












а почему изображений не видно ?
ВідповістиВидалити