Тіла обертання
Будь-яке тіло обертання можна розглядати як результат механічного обертання деякої лінії навколо нерухомої прямої (осі). В математиці механічне обертання замінюється геометричним перетворенням простору, яке називається обертанням або перетворенням простору. Тому тіло обертання - це множина (сукупність) всіх можливих образів деякої лінії l при всіх можливих поворотах простору навколо деякої прямої p.
Лінія 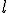 називається твірною, а пряма
називається твірною, а пряма 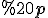 - віссю поверхні обертання.
- віссю поверхні обертання.
Якщо поверхня обертання обмежує деяку кінцеву частину простору, то ця частина разом із поверхнею обертання називається тілом обертання.
Циліндрична поверхня. Циліндр
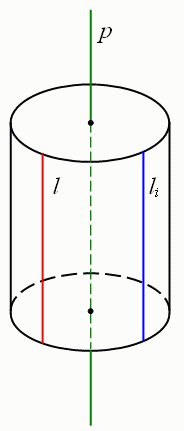
мал. 1
|
Нехай за твірну поверхні обертання вибрано пряму 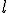 , яка паралельна осі
, яка паралельна осі 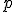 .
.
Означення. Множина всіх прямих, які є образами прямої 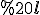 , паралельної прямій
, паралельної прямій 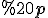 , при всіх можливих поворотах простору з віссю
, при всіх можливих поворотах простору з віссю 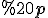 , називають прямою круговою циліндричною поверхнею (мал. 1).
, називають прямою круговою циліндричною поверхнею (мал. 1).
мал. 2
|
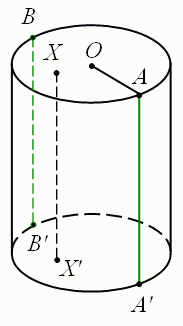
Означення. Циліндром (круговим циліндром) називається тіло, що складається з двох кругів, які не лежать в одній площині і суміщаються паралельним перенесенням, і всіх відрізків, що сполучають відповідні точки цих кругів (мал. 2).
Круги називаються основами циліндра, а відрізки, що сполучають точки кіл кругів - твірними циліндра.
На мал. 2 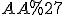 і
і 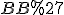 - твірні.
- твірні.
1) Оскільки паралельне перенесення є рух, то основи циліндра рівні.
2) Основи циліндра лежать у паралельних площинах, тому що при паралельному перенесенні площина переходить у паралельну площину.
3) Твірні циліндра паралельні і рівні, тому що при паралельному перенесенні точки зміщуються вздовж паралельних прямих на одну й ту ж саму відстань.
Означення. Циліндр називається прямим, якщо його твірні перпендикулярні до площин основ.
Ми в шкільному курсі будемо розглядати тільки прямий циліндр.
Означення. Радіусом циліндра називається радіус основи (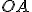 на мал. 2).
на мал. 2).
Означення. Висота циліндра - це відстань між основами циліндра ( на мал. 2).
на мал. 2).
Означення. Вісь циліндра - пряма, що проходить через центри основ.
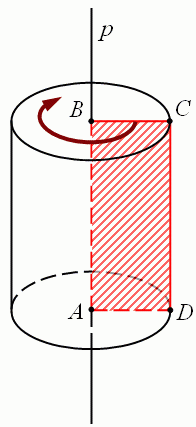
Розташуємо прямокутник так, щоб одна з його сторін належала осі обертання (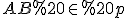 ), тоді сторона
), тоді сторона 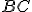 і
і 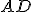 описують круги, а
описують круги, а 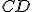 частину циліндричної поверхні.
частину циліндричної поверхні.
Можна вважати, що циліндр отримано шляхом обертання прямокутника 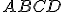 навколо своєї сторони.
навколо своєї сторони.
Частина циліндричної поверхні, утворена стороною прямокутника, називається бічною поверхнею циліндра.
Цилі́ндр (грец. κύλινδρος — «валик») — геометричне тіло, обмежене замкнутою циліндричною поверхнею і двома паралельними площинами, що перетинають її.
Види циліндрів
Нескінченний циліндр — це нескінченне тіло, обмежене замкнутою нескінченною циліндричною поверхнею.
Відкритий циліндр — обмежене замкнутим циліндровим променем і його основою геометричне тіло.
Основи циліндра якісно впливають на циліндр:
- якщо основи циліндра пласкі (і, отже, що містять їх площині рівнобіжні) — циліндр називають таким, що стоїть на площині;
- якщо основи стоять на площині циліндра перпендикулярні твірним — прямий циліндр; зокрема, якщо основа що стоїть на площині циліндра:

Елементи циліндра
Круги що утворюють циліндр називаються основами циліндра. Вони рівні і лежать у паралельних площинах.
Твірні циліндра — відрізки, що сполучають відповідні точки кіл кругів. Вони паралельні і рівні між собою.
Поверхня циліндра складається з основ і бічної поверхні.
Бічна поверхня складається з твірних.
Радіусом циліндра називається радіус його основи.
Висотою циліндра називається відстань між площинами основ.
Віссю циліндра називається пряма, яка проходить через центри основ. Вона паралельна твірним.
Осьовий переріз — переріз циліндра площиною, яка проходить через вісь циліндра.
Дотична до циліндра — площина, яка проходить через твірну прямого циліндра і перпендикулярна до осьового перерізу, проведеного через цю твірну, називається площиною.
Циліндр називається прямим, якщо його твірні перпендикулярні до площин основ. Прямий циліндр можна розглядати як тіло, утворене обертанням прямокутниканавколо його сторони як осі.
Площа поверхні
Площа бічної поверхні
Площа бічної поверхні тіл обертання обчислюється за їхньою розгорткою. Розгортка циліндра являє собою прямокутник з висотою  і довжиною
і довжиною 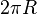 , отже площа бічної поверхні циліндра дорівнює площі його розгортки та обчислюється за формулою:
, отже площа бічної поверхні циліндра дорівнює площі його розгортки та обчислюється за формулою:
 і довжиною
і довжиною 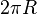 , отже площа бічної поверхні циліндра дорівнює площі його розгортки та обчислюється за формулою:
, отже площа бічної поверхні циліндра дорівнює площі його розгортки та обчислюється за формулою:
Площа загальна
Площа повної поверхні циліндра дорівнює сумі площ його бічної поверхні та його основ:

Об'єм
Візьмемо плоску фігуру, утворену такими прямими: y = R, x = 0, x = h, y = 0 та будемо обертати її навколо осі Ox. Таким чином ми отримуємо тіло обертання, утворене обертанням прямокутника навколо однієї з його сторін, тобто циліндр.
 ,
,
кінцева формула:
 ,
,
де d — діаметр основи; R — радіус основи.

Немає коментарів:
Дописати коментар