Конус.
Приклади задач
№1. Кут між висотою і твірною конуса 60°, висота конуса – H. Знайти площу перерізу, проведеного через дві взаємно перпендикулярні твірні.
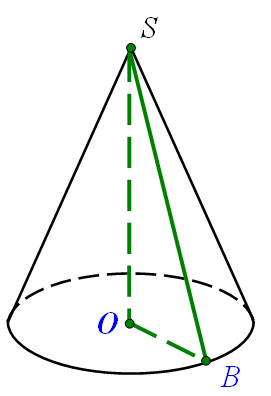
Розв’язання.
Нехай кут між висотою і твірною конуса 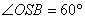 , висота
, висота 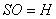 .
.
Нехай існують дві взаємно перпендикулярні твірні, тоді площа цього перерізу буде знаходитись як півдобуток твірних.
З 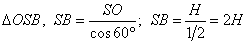 .
.
Отже, 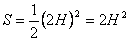 .
.
Відповідь: 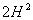 .
.
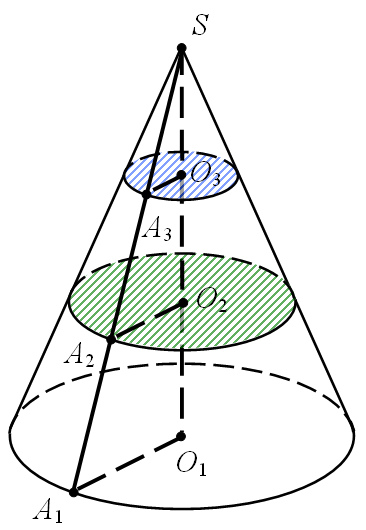 №2. В конусі проведено два перерізи, паралельні основі, які ділять висоту конуса на три рівні частини. Знайти відношення їх площ.
№2. В конусі проведено два перерізи, паралельні основі, які ділять висоту конуса на три рівні частини. Знайти відношення їх площ.
Розв’язання.
Проведемо два перерізи в конусі, паралельно основі, причому так, що центри цих кіл О2 і О3 ділять висоту конуса на три рівні частини. Тоді радіус круга з центром О2 дорівнює 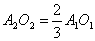 , а радіус круга з центром О3 –
, а радіус круга з центром О3 – 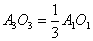 (Це випливає з подібності трикутників
(Це випливає з подібності трикутників 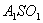 ;
; 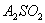 ;
; 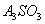 ).
).
Тоді, позначивши площі перерізів 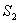 і
і 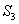 , маємо
, маємо
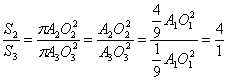 ;
;
або 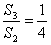 .
.
Відповідь: 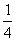 або
або 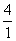 .
.
№3. Радіус основи конуса R, кут нахилу твірної до площини основи - 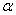 . Площина проходить через вершину конуса і перетинає основу під кутом
. Площина проходить через вершину конуса і перетинає основу під кутом 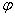 . Знайти площу перерізу.
. Знайти площу перерізу.
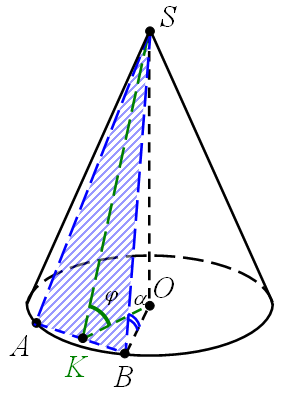
Розв’язання.
Нехай 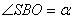 ,
, 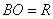 ,
, 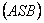 – площина перерізу, що проходить через вершину конуса.
– площина перерізу, що проходить через вершину конуса.
Проведемо 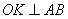 (т. K – середина AB), тоді за теоремою про три перпендикуляри
(т. K – середина AB), тоді за теоремою про три перпендикуляри 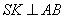 , а отже,
, а отже, 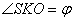 – кут між перерізом та площиною основи. Знайдемо площу
– кут між перерізом та площиною основи. Знайдемо площу  .
.
З 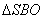 :
: 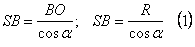
З 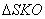 :
: 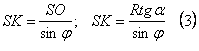
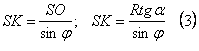
З 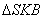 :
: 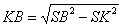 ;
; 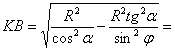
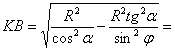
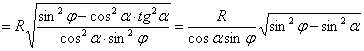 ;
;
Тоді 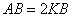 ;
; 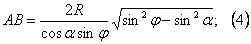
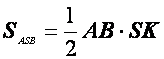 . З рівностей (3); (4)
. З рівностей (3); (4) 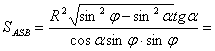
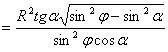 .
.
Відповідь: 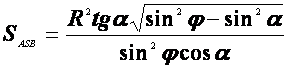 .
.
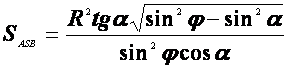 .
.
№4. Точки А, B i C належать різним твірним конуса. Побудуйте точку перетину площини ABC із заданою твірною (або її продовженням), яка не проходить через жодну з даних точок.
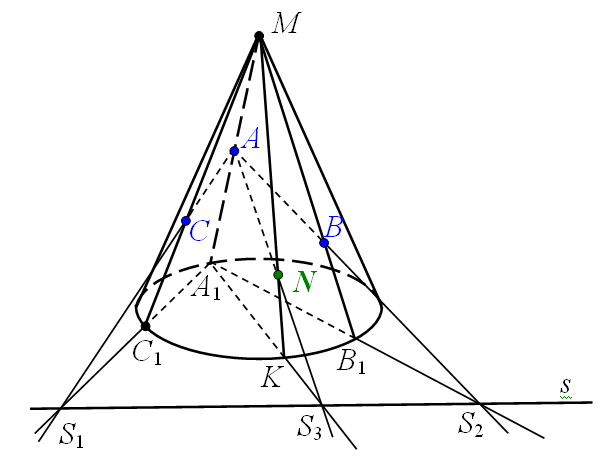
Побудова.
Нехай точки А, B і C належать різним твірним конуса, вони означують деяку площину 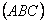 . MK – задана твірна, яка не проходить через жодну з даних точок.
. MK – задана твірна, яка не проходить через жодну з даних точок.
Для побудови скористаємося методом «слідів»:
1) Спроектуємо точки A, B, C в площину основи конуса, отримаємо точки A1, B1, C1.
2) Проведемо через точки A, C та A1, C1 прямі до перетину в т. S1. Аналогічно з точками A, B і A1, B1 до перетину в т. S2.
3) Через точки S1 і S2 проведемо пряму s, яка є слідом січної площини 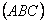 в площині основи конуса.
в площині основи конуса.
4) Сполучимо точки A1 і K, продовжимо до перетину з прямою s в точці S3.
5) Сполучимо точки A і S3, на перетині з твірною MK маємо точку N.
6) N належить площині  , твірній MK, тобто є шуканою.
, твірній MK, тобто є шуканою.
Доведення проведіть самостійно.
№5. Твірна зрізаного конуса дорівнює 2a і нахилена до основи під кутом 60°. Радіус однієї основи вдвічі більше радіуса другої основи. Знайти кожний радіус.
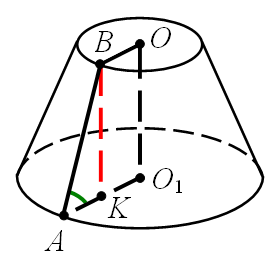
Розв’язання.
Нехай твірна зрізаного конуса 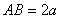 , а кут нахилу твірної до площини основи конус
, а кут нахилу твірної до площини основи конус 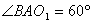 . Користуючись умовою,
. Користуючись умовою, 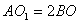 .
.
Опустимо з точки B в площину нижньої основи перпендикуляр, 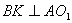 , тоді
, тоді 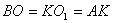 .
.
З 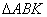 :
: 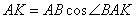 ;
; 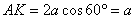 .
.
Тоді 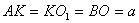 ,
, 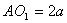 .
.
Відповідь: 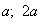 .
.
Немає коментарів:
Дописати коментар