Означення кулі і сфери. Елементи кулі і сфери.
Кулею називають геометричне тіло, утворене обертанням круга навколо осі, що містить його діаметр (мал. 500).

Центр круга, який обертається називають центром кулі, радіус круга - радіусом кулі, а діаметр круга - діаметром кулі. На малюнку 500 точка О - центр кулі, ОА і ОВ - радіуси кулі, а АВ - діаметр кулі.
Поверхню кулі називають сферою.
Центр, радіус та діаметр кулі є також центром, радіусом та діаметром сфери.
Всі точки сфери знаходяться на одній і тій самій відстані, що дорівнює радіусу, від центра сфери. Інші точки кулі, які не належать сфері, називають внутрішніми точками, про такі точки кажуть, що вони лежать всередині сфери. Внутрішні точки кулі знаходяться від центра кулі на відстані, яка менша за радіус.
Таким чином приходимо до ще одного означення сфери і кулі.
Сферою називають поверхню, яка складається із всіх точок простору, рівновіддалених від однієї і тієї самої точки. Цю точку називають центром сфери, а відстань від центра сфери до будь-якої її точки - радіусом сфери.
Кулею називають геометричне тіло, що складається з усіх точок простору, які знаходяться на відстані, не більшій за дану від даної точки. Цю точку називають центром кулі, а дану відстань - радіусом кулі.
Приклад. Радіус сфери дорівнює 3,5 см. Всередині чи зовні сфери розміщена точка А, якщо вона віддалена від центра сфери на: 1)  см, 2)
см, 2)  см.
см.
Розв’язання. 1) Оскільки  < 3,5, то точка А розміщена всередині сфери.
< 3,5, то точка А розміщена всередині сфери.
2) Оскільки  > 3,5, то точка А розміщена зовні сфери.
> 3,5, то точка А розміщена зовні сфери.
Куля в аналітичній геометрії
 — рівняння кулі з центром в точці з координатами
— рівняння кулі з центром в точці з координатами  та радіусом
та радіусом  .
.
 , де
, де  — координати її центра.
— координати її центра.
Площа сфери та об'єм кулі
 , що приблизно дорівнює
, що приблизно дорівнює  .
.
Площа поверхні кулі є найменшою серед площ поверхонь стереометричних тіл з однаковим об'ємом.
Об'єм кулі можна знайти за формулою
Об'єм кулі можна знайти за формулою
 .
.
Переріз кулі площиною
Будь-який переріз кулі площиною є круг. Центр цього круга є основою перпендикуляра, опущеного з центра кулі на січну площину. Радіус такого перерізу визначається формулою
 , де
, де  — радіус кулі,
— радіус кулі,  — відстань від центра кулі до перерізу.
— відстань від центра кулі до перерізу.
Площина, яка проходить через центр кулі, називається діаметральною площиною, переріз нею кулі — великим кругом, а переріз сфери — великим колом. Радіусвеликого круга та великого кола дорівнює радіусові кулі. Будь-яка діаметральна площина кулі є її площиною симетрії.
Частини кулі
Сегмент[ред. • ред. код]
Сегмент кулі — це та її частина, що утворюється внаслідок перерізу площиною. Основними величинами, які характеризують сегмент, є радіус кулі  та довжина перпендикуляра, опущеного на центр перерізу зі сфери,
та довжина перпендикуляра, опущеного на центр перерізу зі сфери,  .Довжина цього перпендикуляра також дорівнює різниці між радіусом
.Довжина цього перпендикуляра також дорівнює різниці між радіусом  і відстанню від центра до перерізу
і відстанню від центра до перерізу  , тобто
, тобто  . Таким чином об'єм сегмента дорівнює
. Таким чином об'єм сегмента дорівнює
 та довжина перпендикуляра, опущеного на центр перерізу зі сфери,
та довжина перпендикуляра, опущеного на центр перерізу зі сфери,  .Довжина цього перпендикуляра також дорівнює різниці між радіусом
.Довжина цього перпендикуляра також дорівнює різниці між радіусом  і відстанню від центра до перерізу
і відстанню від центра до перерізу  , тобто
, тобто  . Таким чином об'єм сегмента дорівнює
. Таким чином об'єм сегмента дорівнює ,
,
а площа поверхні —
Зріз
Зріз — це стереометричне тіло, утворене перерізами кулі двома паралельними площинами. Він характеризується такими величинами:
Об'єм зрізу визначається формулою
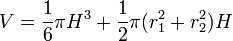 ,
,
а площа поверхні —
 .
.
Сектор
Сектор складається з кульового сегмента та конуса, основа якого збігається з основою сегмента, а вершина — з центром кулі. Сектор характеризують радіус кулі  тадовжина перпендикуляра, опущеного на центр основи конуса зі сфери,
тадовжина перпендикуляра, опущеного на центр основи конуса зі сфери,  . Об'єм сектора:
. Об'єм сектора:
 тадовжина перпендикуляра, опущеного на центр основи конуса зі сфери,
тадовжина перпендикуляра, опущеного на центр основи конуса зі сфери,  . Об'єм сектора:
. Об'єм сектора: .
.
Площа його поверхні:
 .
.
Вписані й описані кулі
Описана куля
Куля називається описаною навколо багатогранника, якщо всі вершини багатогранника лежать на поверхні кулі (сфери). В цьому випадку багатогранник називають вписаним в кулю. Центр кулі, описаної навколо багатогранника, рівновіддалений від всіх його вершин, тобто є точкою перетину площин, проведених через середини ребер багатогранника (призми, піраміди) перпендикулярно до них. Відстань від центра кулі до вершин багатогранника — його радіус.
Вписана куля
Куля називається вписаною в багатогранник, якщо всі грані багатогранника дотикаються до кулі. Багатогранник у цьому випадку називається описаним навколо кулі (сфери). Центр кулі, вписаної у багатогранник, рівновіддалений від усіх його граней. Він є точкою перетину півплощин, проведених через ребра двогранних кутів, утворених двома суміжними гранями, які поділяють цей кут навпіл. Відстань від центра кулі до граней — його радіус.
Додаткові відомості
Куля так само, як циліндр і конус, є тілом обертання. Вона утворюється при обертанні півкруга навколо його діаметра як осі. Цей діаметр називають віссю кулі, а його кінці — полюсами кулі.
Відрізок, який сполучає дві точки кульової поверхні і проходить через центр кулі, називається діаметром. Кінці будь-якого діаметра називаються діаметрально протилежними точками кулі.
Відрізок, який сполучає дві точки кульової поверхні і проходить через центр кулі, називається діаметром. Кінці будь-якого діаметра називаються діаметрально протилежними точками кулі.
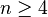 , вона називається
, вона називається 
 .
.
Немає коментарів:
Дописати коментар