Конус. Приклади задач

Приклади задач

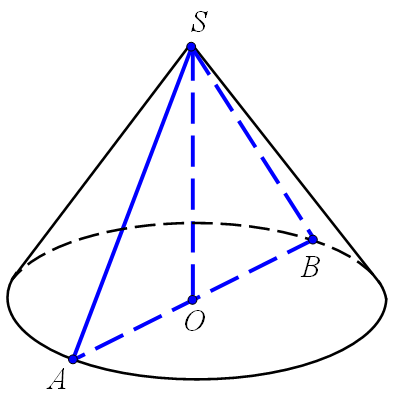
№1. Найбільший кут між твірними конуса дорівнює 60°. Знайти відношення бічної поверхні до площі основи конуса.

Розв’язання.

Нехай 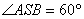 , тоді трикутник  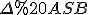– рівносторонній, оскільки за властивостями конуса 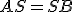. До того ж  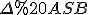 – осьовий переріз, оскільки кут між твірними буде найбільшим лише в цьому випадку.

Отже, .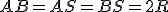

;  .

 .

Відповідь: 2.

№2. Розгорткою бічної поверхні конуса є півкруг. Знайти кут при вершині осьового перерізу.

Розв’язання.

Розглянемо розгортку бічної поверхні конуса на мал.

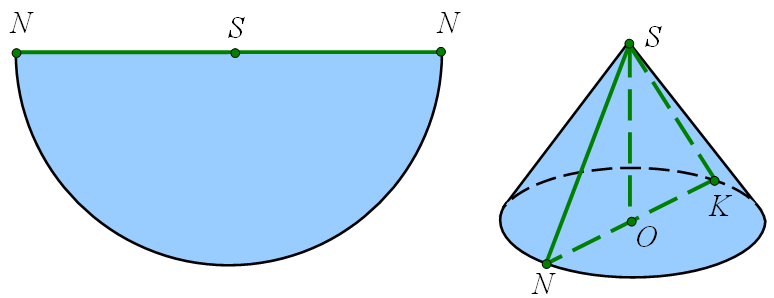
Оскільки розгорткою бічної поверхні є півкруг, то площа бічної поверхні конуса дорівнює половині площі круга радіуса 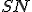, тобто 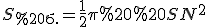. В свою чергу відомо, що площа бічної поверхні конуса обчислюється  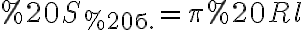, де 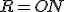 , , 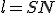тобто

.

Маємо  , .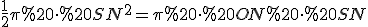

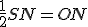Звідси випливає, що у прямокутному 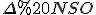, кут 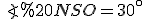, а тоді 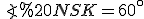, де 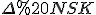– осьовий переріз.

Відповідь: .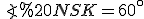

№3. Знайти бічну поверхню зрізаного конуса, якщо його твірна утворює з площиною з основи кут 60°, а площі основ 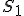 і .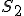

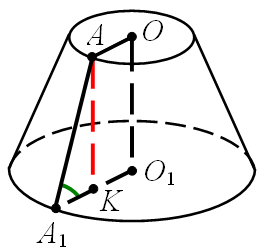
Розв’язання.

Нехай твірна 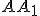 утворює з площиною основи кут 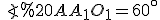, а площа нижньої основи – 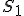, верхньої – .

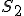Нехай 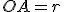 ;  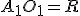, тоді 

 _;  

_;    

 ;    (1)            (2) .

Знайдемо довжину твірної конуса 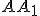 з  :

 _;  ;     ;      (3).

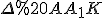Підставимо значення (1); (2); (3) у формулу  ; 

 _.

Відповідь:  .