Правильна піраміда.
 |  |  |
 |  |  |
Піраміду називають правильною, якщо її основою є правильний многокутник, а основи висоти збігаються із центром цього многокутника.
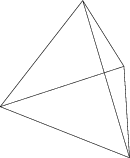
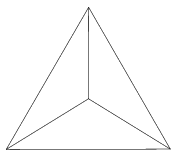
Нагадаємо, що центром правильного многокутника називають центр описаного навколо нього (або вписаного в нього) кола. На малюнку 466 зображено правильну трикутну піраміду, а на малюнку 467 - правильну чотирикутну піраміду, висоти яких - відрізки QК; точка К - центр правильного многокутника, що лежить в основі піраміди.

Віссю правильної піраміди називають пряму, яка містить її висоту.
Властивості правильної піраміди:
1) Усі бічні ребра правильної піраміди рівні.
2) Усі бічні грані правильної піраміди - рівні рівнобедрені трикутники.
3) Усі апофеми правильної піраміди рівні між собою.
Теорема про бічну поверхню правильної піраміди
Приклад. Сторона основи правильної трикутної піраміди дорівнює 6 см, а висота - 2 см. Знайти довжину бічного ребра.
Розв’язання. 1) (мал. 466) Нехай QАВС - правильна піраміда, QК = 2 см - висота піраміди.
2) Оскільки точка К - центр описаного навколо трикутника АВС кола, то КВ = R - радіус цього кола. За відомою формулою R = a /3, де а = АВ = 6 см - сторона основи. Отже,
/3, де а = АВ = 6 см - сторона основи. Отже,
Правильний тетра́едр
Тетра́едр називається правильним, якщо всі його грані — рівносторонні трикутники. У правильного тетраедра всі двогранні кути при ребрах і всі тригранні кути при вершинах рівні.

Декартові координати
Правильний тетраедр можна задати координатами його вершин
- (1, 1, 1)
- (-1, −1, 1)
- (-1, 1, −1)
- (1, −1, −1)
довжина ребра в цьому випадку складатиме  .
.
 .
.Формули
У правильного тетраедра з довжиною ребра a:
Площа поверхні 

Висота 

Радіус вписаної сфери 

Радіус описаної сфери 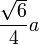
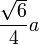
Кут нахилу ребра 

Кут нахилу грані 

Група симетрій — Тетраедральна (Th)
Властивості правильного тетраедра
- В правильний тетраедр можна вписати октаедр, притому чотири (з восьми) грані октаедра будуть суміщено з чотирма гранями тетраедра, всі шість вершин октаедра будуть суміщено з центрами шести ребер тетраедра.
- Правильний тетраедр з ребром х складається з одного вписаного октаедра (у центрі) з ребром х/2 і чотирьох тетраедрів (по вершинам) з ребром х/2.
- Правильний тетраедр можна вписати в куб двома способами, притому чотири вершини тетраедра будуть суміщено з чотирма вершинамі куба. Всі шість ребер тетраедра лежатимуть на всіх шести гранях куба і дорівнюватимуть діагоналі грані-квадрата.
- Правильний тетраедр можна вписати в ікосаедр, притому, чотири вершини тетраедра будуть суміщено з чотирма вершинамі ікосаедра.
Чотиригранник, тетраедр, трикутна піраміда — багатогранник із чотирма вершинами, і з чотирма трикутними гранями, в кожній з вершин якого сходяться по 3 грані.
У чотиригранника 4 грані, 4 вершини і 6 ребер. Паралельні площини, що проходять через парчотиригранника, що схрещуються, визначають описання чотиригранника паралелепіпед.
Відрізок, що сполучає чотиригранника з точкою перетину медіан протилежної грані, називається його медіаною, опущеною з даної вершини. Відрізок, що сполучає середини чотиригранника, що схрещуються, називається його бімедіаною, що сполучає дані ребра. Відрізок, що сполучає чотиригранника з точкою протилежної грані і перпендикулярний цій грані, називається його висотою, опущеною з даної вершини.
Властивість
Всі медіани і бімедіани чотиригранника перетинаються в одній точці. Ця точка ділить медіани у відношенні 3:1, міряючи від вершини, а бімедіани — навпіл.
Види тетраедрів
Виділяють:
- рівногранний тетраедр, у якого всі грані - рівні між собою трикутники;
- ортоцентричний тетраедр, у якого всі висоти, опущені з вершин на протилежні грані, перетинаються в одній точці;
- прямокутний тетраедр, у якого всі ребра, прилеглі до однієї з вершин, перпендикулярні між собою;
- правильний тетраедр, у якого всі чотири грані - рівносторонні трикутники.
Об'єм[ред. • править текст]
Об'єм чотиригранника (з урахуванням знаку), вершини якого знаходяться в точках  ,
,  ,
,  ,
,  , дорівнює
, дорівнює
 ,
,  ,
,  ,
,  , дорівнює
, дорівнює
 ;
;  ,
,
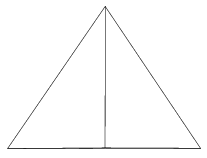
 є точка перетину його бісектрис, котрі водночас є висотами і медіанами. Медіани при паралельному проектуванні зображуються медіанами. Тому будуємо дві медіани основи. Точка їх перетину — основа висоти піраміди. Зображуємо висоту, а потім з’єднуємо вершину піраміди з вершинами основи. Отримаємо бічні ребра.
є точка перетину його бісектрис, котрі водночас є висотами і медіанами. Медіани при паралельному проектуванні зображуються медіанами. Тому будуємо дві медіани основи. Точка їх перетину — основа висоти піраміди. Зображуємо висоту, а потім з’єднуємо вершину піраміди з вершинами основи. Отримаємо бічні ребра. — кут нахилу бічного ребра до площини основи (однаковий для всіх ребер);
— кут нахилу бічного ребра до площини основи (однаковий для всіх ребер);  — кут нахилу бічної грані до площини основи (однаковий для всіх граней).
— кут нахилу бічної грані до площини основи (однаковий для всіх граней). .
. ;
;  ;
;  ;
; ;
;  ;
;  .
. .
. ;
;  .
. , то ON є відстанню від основи висоти не тільки до анафеми, а й до бічної грані BSC.
, то ON є відстанню від основи висоти не тільки до анафеми, а й до бічної грані BSC. .
. ;
; ;
; ;
; ;
; .
.
 ,
,  , тобто
, тобто  .
. ;
;  .
. ;
;  .
.
 ;
; ;
; ;
;
 .
. ;
;  .
.

Немає коментарів:
Дописати коментар