Циліндр. Приклади задач

Циліндр. Приклади задач 

№ 1. Площа основи циліндра відноситься до площі осьового перерізу як 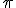 і 4. Знайти кут між діагоналями осьового перерізу.

Розв'язання.

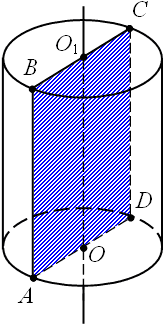Розглянемо осьовий переріз ABCD. Твірна циліндра AB дорівнює його висоті, а відрізок AD є діаметром циліндра, тоді площа перерізу буде  В основі циліндра лежить круг, площа якого дорівнює  За умовою задачі можна записати співвідношення Бачимо, що висота циліндра дорівнює діаметру, тобто ABCD - квадрат. Як відомо, діагоналі квадрата перетинаються під прямим кутом. Відповідь: 90°.

№2.  В циліндрі радіуса R і висоти H проведено переріз, паралельний осі циліндра. На якій відстані від осі знаходиться площина перерізу, якщо його площа дорівнює S?

Розв'язання.

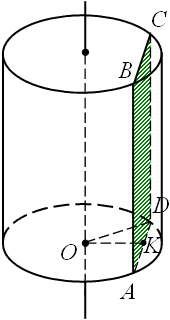Відомо, що переріз циліндра площиною, яка паралельна осі циліндра, є прямокутник. Розглянемо прямокутник ABCD. Його площа S, CD=H,  тоді . Опустимо з точки О - центра основи циліндра перпендикуляр на відрізок AD. Оскільки вісь паралельна перерізу, то OK - відстань від осі до перерізу. AK=KD. Розглянувши трикутник OKD, маємо:  Відповідь:

№3. Діагональ розгортки бічної поверхні циліндра дорівнює d утворює з висотою розгортки кут 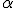. Знайти площі основ і осьового перерізу циліндра.

Розв'язання.

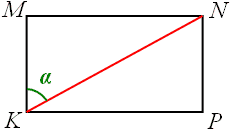Розглянемо розгортку бічної поверхні циліндра, це прямокутник, позначимо його KNMP.Тоді KN - діагональ розгортки, KN=d;  KM - висота;   З         В свою чергу , отже, Площа основи циліндра знайдемо за формулою       З : ;  площа осьового перерізу - це добуток висоти циліндра на діаметр його основи (див. задачу №1), отже, Відповідь.

№4. У нижній основі циліндра проведено хорду, яка знаходиться на відстані d від центра верхньої основи. Із центра нижньої основи її видно під кутом 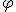. Відрізок, який сполучає центр верхньої основи з точкою кола нижньої основи, утворює з нижньою основою кут 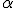. Знайти площу бічної поверхні циліндра.

Розв'язання.

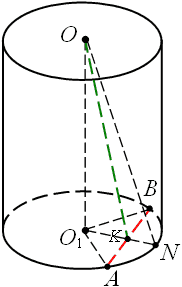Нехай у циліндрі точки O і O1 - центри верхньої і нижньої основ відповідно, AB - хорда в нижній основі циліндра, OK - відстань від центра верхньої основи до хорди AB,   N  - точка в нижній основі,  - кут між відрізком ON та площиною нижньої основи. Покладемо  тоді з  Оскільки  тоді за теоремою про три перпендикуляри  Враховуючи, що  - рівнобедрений,  та O1K - бісектриса. Розглянемо  в ньому  А з  маємо: Прирівняємо праві частини рівностей (1) та (2), попередньо піднісши до квадрату рівність (1), маємо Підставимо отримане значення в рівність (1): Бічна поверхня циліндра буде обчислюватись за формулою , тоді запишемо Відповідь.