Правильний тетраедр

Правильний тетраедр

Тетра́едр називається правильним, якщо всі його грані — рівносторонні трикутники. У правильного тетраедра всі двогранні кути при ребрах і всі тригранні кути при вершинах рівні.

Правильний тетраедр має три вісі симетрії.

Правильний тетраедр має шість площин симетрій.

Декартові координати

Правильний тетраедр можна задати координатами його вершин

• (1, 1, 1)
• (-1, −1, 1)
• (-1, 1, −1)
• (1, −1, −1)

довжина ребра в цьому випадку складатиме 
.

Формули

У правильного тетраедра з довжиною ребра a:

Площа поверхні 

Об'єм 

Висота 

Радіус вписаної сфери 

Радіус описаної сфери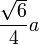 

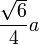
Кут нахилу ребра 

Кут нахилу грані 

Група симетрій — Тетраедральна (T_h)

Властивості правильного тетраедра

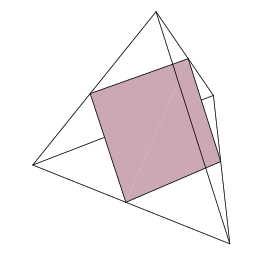
• В правильний тетраедр можна вписати октаедр, притому чотири (з восьми) грані октаедра будуть суміщено з чотирма гранями тетраедра, всі шість вершин октаедра будуть суміщено з центрами шести ребер тетраедра.
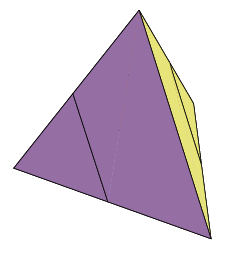
• Правильний тетраедр з ребром х складається з одного вписаного октаедра (у центрі) з ребром х/2 і чотирьох тетраедрів (по вершинам) з ребром х/2.
• Правильний тетраедр можна вписати в куб двома способами, притому чотири вершини тетраедра будуть суміщено з чотирма вершинамі куба. Всі шість ребер тетраедра лежатимуть на всіх шести гранях куба і дорівнюватимуть діагоналі грані-квадрата.
• Правильний тетраедр можна вписати в ікосаедр, притому, чотири вершини тетраедра будуть суміщено з чотирма вершинамі ікосаедра.

Теорема про бічну поверхню правильної піраміди

Піраміда називається правильною, якщо її основою є правильний многокутник, а основа висоти збігається з центром многокутника. Віссю правильної піраміди називається пряма, яка містить її висоту. Бічні ребра правильної піраміди рівні, бічні грані — рівні рівнобедрені трикутники. Висота бічної грані, проведена з вершини піраміди, називається апофемою. Вона є бісектрисою та медіаною бічної грані, оскільки та є рівнобедреним трикутником.
Теорема. Бічна поверхня правильної піраміди дорівнює добутку півпериметра основи на апофему.
; ,
де Р — периметр основи, а — сторона основи, l — довжина апофеми.
Правильна трикутна піраміда

В основі правильної трикутної піраміди лежить рівносторонній трикутник, який зображується довільним трикутником (див. рисунок).

Центром  є точка перетину його бісектрис, котрі водночас є висотами і медіанами. Медіани при паралельному проектуванні зображуються медіанами. Тому будуємо дві медіани основи. Точка їх перетину — основа висоти піраміди. Зображуємо висоту, а потім з’єднуємо вершину піраміди з вершинами основи. Отримаємо бічні ребра.
На рисунку:  — кут нахилу бічного ребра до площини основи (однаковий для всіх ребер);  — кут нахилу бічної грані до площини основи (однаковий для всіх граней).
Нехай .
Тоді ; ; ;
; ; .
Отже, .
; .
Площина осьового перерізу ASD є площиною симетрії правильної трикутної піраміди.
Ця площина перпендикулярна до площини основи і площини грані BSC.
Цікаво також відмітити, що мимобіжні ребра піраміди (SA і BC, SB і AC, SC і AB) є перпендикулярними. Якщо , то ON є відстанню від основи висоти не тільки до анафеми, а й до бічної грані BSC.
.

Правильна чотирикутна піраміда

В основі правильної чотирикутної піраміди лежить квадрат, який зображується довільним паралелограмом. Його центром є точка перетину діагоналей. Ця точка — основа висоти піраміди.
Нехай сторона квадрата а (див. рисунок).
Тоді ;
;
;
;
.

Зверніть увагу: , , тобто .
При паралельному проектуванні паралельність зберігається.
; .
Відстань від основи висоти до бічної грані:
; .

Правильна шестикутна піраміда

В основі правильної шестикутної піраміди лежить правильний шестикутник (див. рисунок). Його центром є точка перетину діагоналей. Ця точка — основа висоти піраміди.
Тоді ;
Нехай сторона правильного шестикутника а.
;
;

.
; .