Обчислення об’ємів тіл обертання (циліндра, конуса)
за допомогою визначеного інтегралу
Скористаємося формулою обчислення об’ємів тіл обертання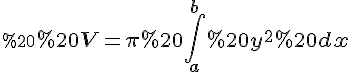 
, яка доводиться у курсі математичного аналізу.
Розв’яжемо декілька задач.
Задача 1. Довести, що об’єм циліндра обчислюється за формулою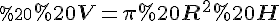 
, де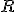 
– радіус основи, 
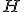– висота циліндра.
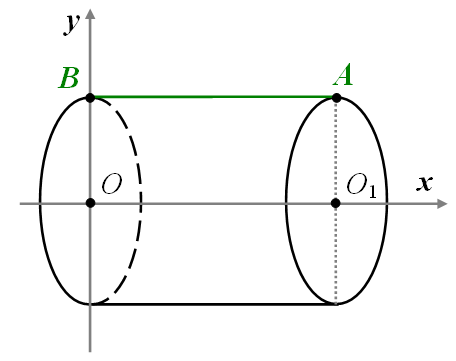
Розв’язання.
Розташуємо циліндр в декартовій системі координат так, як зображено на малюнку: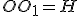 
, 
.
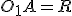Циліндр отримано шляхом обертання прямокутника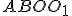 
навколо осі 
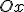. Оскільки 
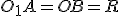, то пряма 
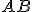задається рівнянням 
.
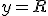Тоді
Задача 2. Довести, що об’єм конуса обчислюється за формулою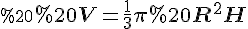 
.
Розв’язання.
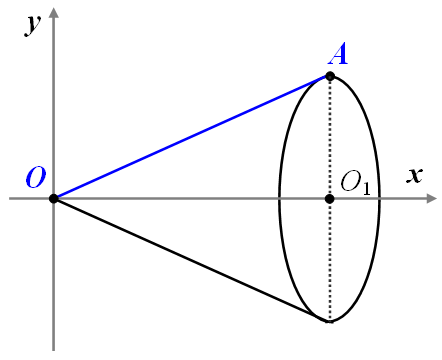
Будемо обертати відрізок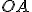 
навколо осі 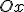(див. мал.). Отримаємо конус, у якого , .
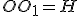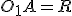Пряма 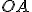задається рівнянням 
.
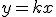Знайдемо кутовий коефіцієнт
Тоді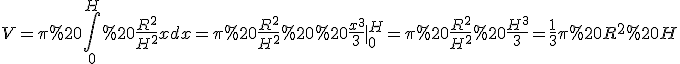 
.
Немає коментарів:
Дописати коментар