Тіла обертання. Приклади задач


Тіла і поверхні обертання.
Нехай деякий плоский опуклий многокутник АВСDК обертається навколо нерухомої прямої, що містить сторону АВ (мал. 481). Тоді кожна точка, що належить многокутнику, крім точок, що належать стороні АВ, описує коло, центр якого належить прямій АВ. При цьому весь многокутник АВСDК описує тіло обертання, пряму АВ називають віссю обертання цього тіла.

Площина, що проходить через вісь тіла обертання, перетинає його по деякій фігурі. Цю фігуру називають осьовим перерізом.
Осьовим перерізом тіла обертання, що зображено на малюнку 481 є многокутник СDКК1D1С1.
Поверхню, утворену обертанням ламаної ВСDКА навколо прямої АВ називають поверхнею обертання.
Якщо тіло обертання, що утворене обертанням многокутника АВСDК перетнути площиною перпендикулярною прямій АВ, то в перерізі отримаємо круг, центр якого належить прямій АВ.
Таким чином приходимо до означення тіла обертання (у найпростішому випадку), яким будемо користуватись у шкільному курсі геометрії.
Тілом обертання називають таке тіло, яке площинами, перпендикулярними до деякої прямої (осі обертання), перетинається по кругах з центрами на цій прямій.
В загальному виді: тілом обертання називають геометричне тіло, утворене обертанням деякої плоскої фігури навколо фіксованої прямої, яку називають віссю обертання.
Прикладами тіл обертання у побуті є іграшки (наприклад, матрьошка, м’яч), бочки, діжки тощо (мал. 482).

Приклад. Прямокутник, діагональ якого дорівнює 10 см, а одна із сторін на 2 см менша за іншу, обертається навколо більшої сторони прямокутника. Знайти радіус та висоту отриманого циліндра.
Розв’язання. 1) Нехай прямокутник АОО1А1 обертається навколо осі OO1, OO1 > ОА (мал. 483).
2) Позначимо ОА = х см, тоді OO1 = (х + 2) см. За умовою O1А = 10 см. Маємо х2 + (х + 2)2 = 102; 2x2 + 4x - 96 = 0; x2 + 2x - 48 = 0; x1 = 6; х2 = -8. Враховуючи х > 0, маємо х= = 6 см.
3) Отже, радіус циліндра ОА = 6 см, а висота АА1 = OO1 = 6 + 2 = 8 (см).
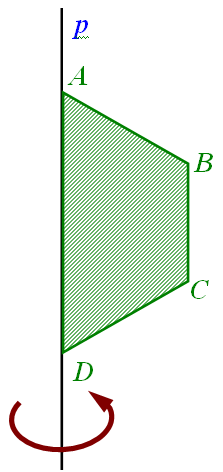
№1. ABCD – трапеція, описана навколо кола. AB=CD; AD=8; BC=2. Знайти об’єм тіла, утвореного шляхом обертання трапеції навколо більшої основи.
Розв’язання
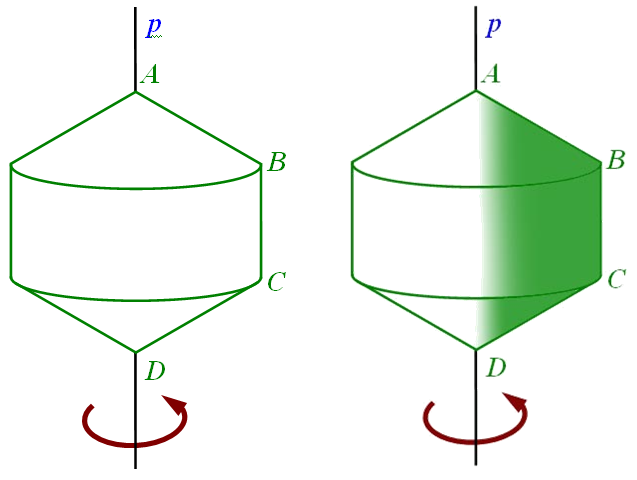
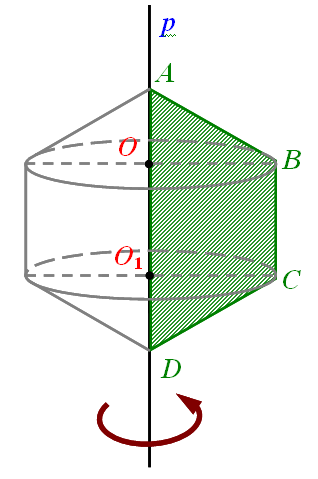 |
1)
Знайдемо
2)
Тоді
Відповідь:
|
№2. Трикутник зі сторонами 4 см; 13 см; 15 см обертається навколо меншої сторони.
Знайти: 1) площу поверхні тіла обертання;
2) об’єм тіла обертання.

Розв’язання (див. мал. 3)
1)
|
Знайдемо
|
2)
|
Відповідь: 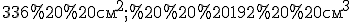 .
.
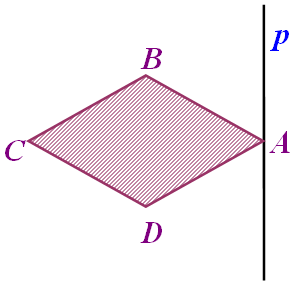
№3. 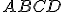 – ромб,
– ромб, 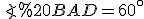 ,
, 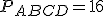 . Знайти об’єм тіла, утвореного обертанням ромба навколо осі, що проходить через вершину
. Знайти об’єм тіла, утвореного обертанням ромба навколо осі, що проходить через вершину 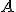 перпендикулярно діагоналі.
перпендикулярно діагоналі.
Розв’язання
Використовуючи симетрію відносно площини більшого круга, обчислимо спочатку об’єм зрізаного конуса, віднімемо об’єм конуса з твірною  , потім збільшимо цю величину вдвічі.
, потім збільшимо цю величину вдвічі.
1) ) ;
;
З  :
: 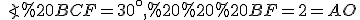 (1)
(1)
Підставимо значення (1), (2) і (3):
2) 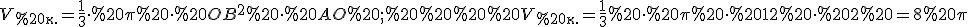 .
.
Врахувавши симетрію, маємо: 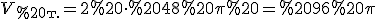 .
.
Відповідь: 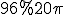 .
.
Немає коментарів:
Дописати коментар