Пряма кругова конічна поверхня
Розглянемо ще приклад поверхні обертання, твірна якої є прямою лінією, але тепер вона перетинає вісь обертання.
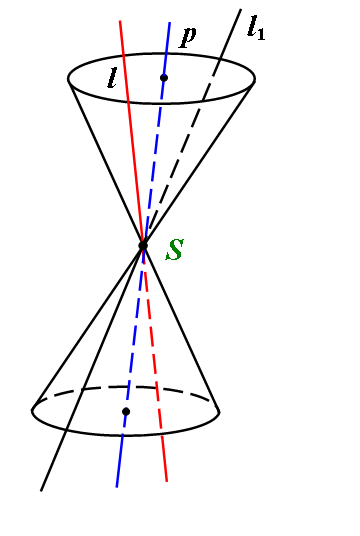
Означення. Множина всіх прямих, які є образами прямої l при всіх можливих поворотах простору навколо осі p, яка перетинається з l в точці S, називається прямою круговою конічною поверхнею.
В подальшому будемо скорочено називати цю поверхню просто конічною.
Точка S, в якій перетинаються прямі l і p, називаються вершиною конічної поверхні; пряма l і всі її образи при всіх можливих поворотах простору навколо p – твірні конічні поверхні; пряма p – вісь конічної поверхні.
Конус
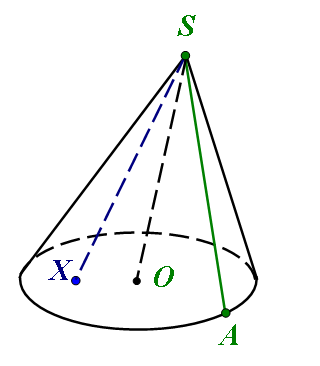
Означення. Конусом (круговим конусом) називається тіло, яке складається з круга, точки, що не лежить в площині цього круга і всіх відрізків, що з’єднують цю точку з точками основи.
Круг з центром в точці О – основа; S – вершина; SA – твірна конуса.
Поверхня конуса складається з основи і конічної поверхні (бічної поверхні).
Означення. Конус називається прямим, якщо пряма, що сполучає вершину з центром основи, перпендикулярна основі.
В подальшому ми будемо розглядати тільки прямий конус. Прямий круговий конус можна уявити собі як тіло, отримане при обертанні прямокутного трикутника навколо катета (див. мал.).
Частина конічної поверхні, утворена гіпотенузою цього трикутника, називається бічною поверхнею конуса.
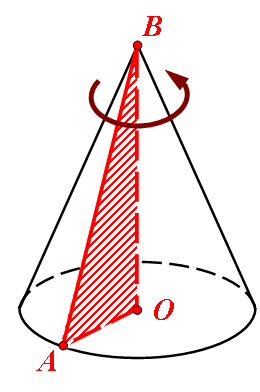
Означення. Висотою називається перпендикуляр, опущений з вершини конуса на площину основи.
На мал. BO – висота.
У прямого конуса основа висоти співпадає з центром основи. У конуса пряма, що містить висоту, є віссю конуса.
Немає коментарів:
Дописати коментар