середу, 9 липня 2014 р.

Прямокутний тетраедр

Прямокутний тетраедр

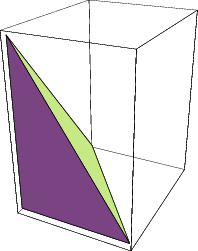TrirectangularTetrahedronTrirectangularTetraWire
Прямокутний тетраедр - це чотиригранник у якого всі ребра, прилеглі до однієї з вершин, перпендикулярні між собою.
У прямокутному тетраедрі завжди три прилеглі грані будуть прямокутними трикутниками, а остання грань будедовільним трикутником.

Результаты поиска


Формули

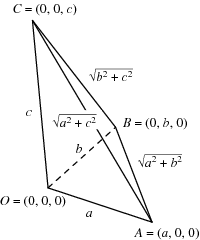
У прямокутного тетраедра з перпендикулярними гранями a, b, c та вершиною в точці перетину перпендикулярних ребер (прямокутний тригранний кут):
  • ~ V = \frac16abc (об'єм тетраедра);
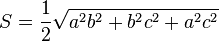  • ~ S = \frac12\sqrt{a^2b^2+b^2c^2+a^2c^2} (площа основи тетраедра); Носить назву теореми де Гуа.
  • ~ h = \frac{abc}{2S}; \frac{1}{h} = \frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{b^2} (висота тетраедра з вершини прямокутний тригранний кут на основу, де S це площа основи тетраедра);
  • ~ R = \frac12\sqrt{a^2+b^2+c^2} (радіус сфери описаної навколо тетраедра);
  • ~ r = \frac{ab+bc+ac+\sqrt{a^2+b^2+c^2}}{2(a+b+c)} (радіус сфери вписаної в тетраедр);
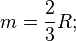
  • ~ m = \frac23R; ~ m = \frac13\sqrt{a^2+b^2+c^2} (медіана проведена з вершини прямокутний тригранний кут, де R це радіус сфери описаної навколо тетраедра);

Прямокутний тетраедр та інші геометничні фігури


Тетраедр (або трикутна піраміда) має схожість з трикутником.Вивчаючи просторові фігури, корисно порівнювати їх з більш плоскими фігурами. Пряма і площина, паралелограм і паралелепіпед, окружність і сфера мають подібними властивостями.
Трикутник є багатокутник з найменшим числом сторін, тетраедр - багатогранник з найменшим числом граней.
Тетраедр - складніша фігура, ніж трикутник, і не дивно, що його властивості більш різноманітні.
Розглянемо один спеціальний вид тетраедра - прямокутний тетраедр. Нехай дано прямокутний паралелепіпед
Через кінці трьох його ребер, що виходять з однієї вершини, проведемо площину. Ця площина відсікає від прямокутного паралелепіпеда тетраедр DABC, у якого всі плоскі кути при вершині D прямі (тригранний кут при вершині D прямий). Такий тетраедр називається прямокутним. Грань АВС будемо називати підставою, а ребра AD, BD, CD - бічними ребрами тетраедра.
Подібно до того, як прямокутний трикутник можна добудувати до прямокутника, провівши через вершини гострих кутів прямі, паралельні катетам, всякий прямокутний тетраедр можна доповнити до прямокутного паралелепіпеда, якщо через його вершини А, В, С провести площині, паралельні протилежних гранях тетраедра

.
Опубліковано о

Немає коментарів:

Дописати коментар

Підписатися на: Дописати коментарі (Atom)