Циліндр. Тренувальні вправи

Тренувальні вправи

№1. Осьовий переріз циліндра - квадрат, діагональ якого дорівнює 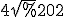 см. Обчислити об'єм циліндра. 

а) 48 см³;     б)  см³;    в) см³;  г) інша відповідь. 

а)
б)
в)
г)

№2. Осьовим перерізом циліндра є квадрат, площа якого дорівнює 16см². Обчислити повну поверхню циліндра.

а) 48 см²;      б) 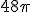 см²;    в)  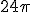см²;  г)  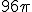см²;    д) інша відповідь.

а)
б)
в)
г)
д)

№3. З 1,1м² заліза виготовили циліндричну трубу діаметром 0,5 м. Знайти довжину труби.
а) ≈ 0,5 м;    б) ≈ 0,7 м;   в)  0,9 м;  г) інша відповідь.

а)
б)
в)
г)

№4. Площа бічної поверхні циліндра - 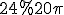 см², а його об'єм дорівнює  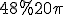см³. Знайти його висоту.

а)  4см;    б) 3 см;   в) інша відповідь.

а)
б)
в)

№5. Осьовим перерізом циліндра є прямокутник, площа якого 72 см². Знайти об'єм циліндра, якщо радіус основи дорівнює 3 см.

а) 108 см³;   б) 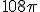см³;   в)  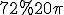см³;    г) інша відповідь.

а)
б)
в)
г)

№6. Площа бічної поверхні циліндра дорівнює 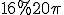см². Знайти площу осьового перерізу циліндра.

а) 16 см²;    б) 8 см²;      в) інша відповідь.

а)
б)
в)

Розв'яжи наступні задачі і впиши відповідь

№7. У циліндрі на відстані 8 см від його осі і паралельно до неї проведено переріз, діагональ якого дорівнює 13 см. Обчислити радіус основи циліндра, якщо його висота дорівнює 5 см.

 

№8. У циліндрі відрізок, який сполучає центр верхньої основи з точкою кола нижньої основи, нахилений до основи під кутом 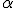. Визначити об'єм циліндра, якщо відстань від центра нижньої основи до середини цього відрізка дорівнює а.

№9. Циліндр перетнуто площиною, паралельною осі так, що в перерізі утворився квадрат з діагоналлю - 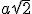 см. Переріз відтинає від кола основи дугу в 60°. Знайти площу повної поверхні циліндра.

№10. Діагоналі осьового перерізу циліндра перетинаються під кутом 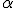. Периметр перерізу дорівнює Р. Знайти об'єм циліндра.

№11. Паралельно осі циліндра, бічна поверхня якого Q, проведено площину. Діагональ утвореного перерізу нахилена до площини основи під кутом 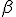. Визначити площу перерізу, якщо відрізок, який сполучає центр основи циліндра з точкою кола іншої основи, утворює з площиною основи кут .

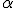№12. Розгорткою бічної поверхні циліндра є прямокутник, одна із сторін якого вдвічі більша від другої. Бічна поверхня циліндра дорівнює 20 дм². Визначити його повну поверхню, якщо твірна циліндра - менша сторона його розгортки.

№13. У циліндрі паралельно його осі проведено площину, що перетинає нижню основу по хорді, яка стягує дугу 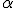. Цю хорду видно із центра верхньої основи під кутом 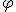. Знайти площу перерізу, якщо радіус циліндра R.