Площа бічної поверхні конуса. Площа поверхні зрізаного конуса

Площа бічної поверхні конуса.

Площа поверхні зрізаного конуса

Якщо кількість сторін основи правильної піраміди необмежено зростає (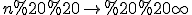), то бічна поверхня цієї піраміди все менше і менше відрізняється від бічної поверхні конуса.

Означення. Площею бічної поверхні конуса є границя, до якої прямує площа бічної поверхні вписаних в конус правильних n-кутних пірамід, коли n необмежено зростає.

Теорема. Площа бічної поверхні конуса дорівнює половині добутку довжини кола його основи на твірну конуса.

Доведення.

Площа бічної поверхні правильної n-кутної піраміди обчислюється , де 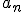– сторона основи піраміди,  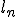– апофема бічної грані.

Далі,  .

Вираз у перших дужках дорівнює довжині кола основи конуса, у других – довжині твірної конуса. Отже,  .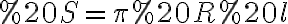

Теорему доведено.

Площа бічної поверхні зрізаного конуса може бути знайдена як різниця площ бічних поверхонь двох конусів.

Введемо позначення.

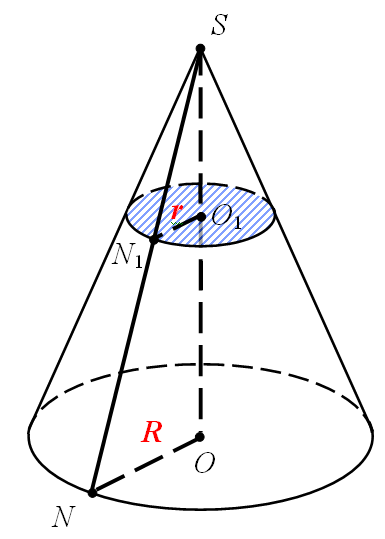Нехай ,  ,  ,    , тоді .

Виразимо 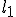 та 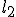 через довжину твірної зрізаного конуса  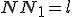та радіуси його основ.

В силу гомотетичності основ зрізаного конуса:

 або

.

Звідси 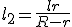. Але 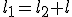, а отже, .

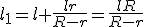Таким чином,

.

Ця формула дозволяє знайти площу бічної поверхні зрізаного конуса за основними його параметрами: радіусами основ і довжиною твірної.

Легко вивести формули площі повної поверхні конуса:

 та зрізаного конуса:

 .