Вписана і описана піраміда

Вписана і описана піраміда

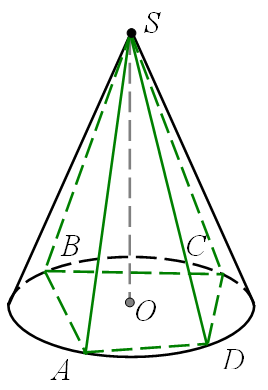Означення. Пірамідою, вписаною в конус, називається така піраміда, основою якої є многокутник, вписаний в коло основи конуса, а вершиною є вершина конуса. Бічні ребра піраміди, вписаної в конус, є твірними конуса.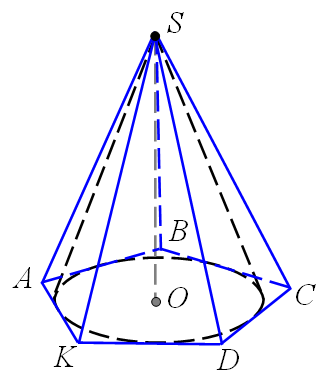

 – вписана піраміда в конус.

 – основа піраміди ( – чотирикутник, вписаний в коло основи конуса).

 – вершина конуса і піраміди.

 – твірна конуса і бічні ребра піраміди.

Означення. Пірамідою, описаною навколо конуса, називається піраміда, у якої основою є многокутник, описаний навколо основи конуса, вершина конуса співпадає з вершиною піраміди. Площини бічних граней піраміди є дотичними площинами конуса.

Зауваження. Повтори означення дотичної площини до циліндра.

Безумовно, не навколо кожного многокутника можна описати коло або вписати коло. Для цього існують певні умови.

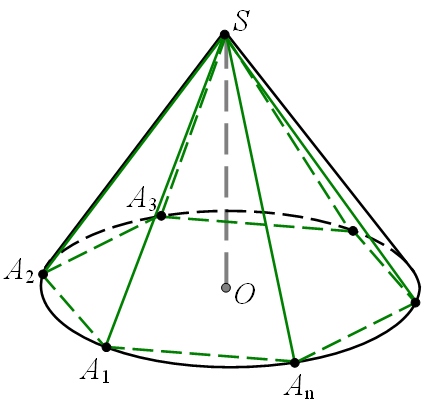
Теорема. У будь-який конус можна вписати правильну піраміду з будь-якою наперед заданою кількістю вершин її основи.

Доведення.

Впишемо в основу конуса правильний многокутник 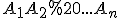 (див. мал.). З’єднаємо його вершини з вершиною конуса. В результаті отримаємо правильну піраміду .

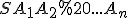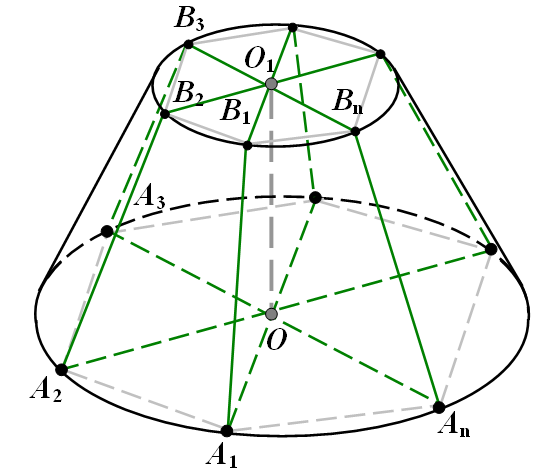Таким же чином в зрізаний конус можна вписати правильну зрізану піраміду.

Зробити це можна наступним чином:

1)      Вписуємо в одну з основ конуса, наприклад, в нижню (більшу) правильний n–кутник .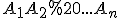

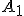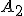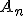
2)      З’єднуємо кожну з вершин  і  ; …    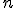 –кутника з центром цієї основи (точка ).

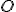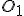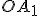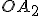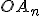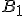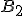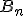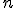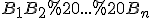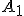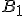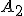3)     Через центр іншої основи (точку ) проводимо радіуси, відповідно паралельні  радіусам , , …,  нижньої основи. Тоді на колі верхньої основи отримуємо точки , , …, , сполучивши які послідовно, маємо правильний -кутник , вписаний у верхню основу. Сполучаємо точки  і ,  і 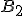  і т.д. Отримана правильна зрізана піраміда  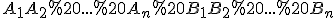– вписана в зрізаний конус.

Існують твердження:

Теорема. Для того, щоб навколо піраміди можна було описати конус, необхідно і достатньо, щоб бічні ребра піраміди мали однакову довжину.

Теорема. Для того, щоб в піраміду можна було вписати конус, необхідно і достатньо, щоб в основу піраміди можна було вписати коло, а основа висоти піраміди була центром цього кола.