Перерізи циліндра

Перерізи циліндра

Перерізи циліндра площинами.

Переріз циліндра площиною, яка проходить через його вісь, називають осьовим перерізом циліндра (мал. 484). Осьовий переріз циліндра — прямокутник, одна із сторін якого дорівнює діаметру циліндра, а інша - його висоті. На малюнку 484 прямокутник АВВ₁А₁ - осьовий переріз циліндра; АВ - діаметр циліндра; АА₁ - твірна, що дорівнює висоті циліндра. Якщо осьовим перерізом циліндра є квадрат, його інколи називають рівнобічним (або рівнобедреним або рівностороннім).

Приклад 1. Довжина кола основи циліндра дорівнює 12 π см, а діагональ осьового перерізу - 13 см. Знайти твірну циліндра.

Розв’язання. 1) Нехай А₁В - діагональ осьового перерізу циліндра (мал. 484); А₁В = 13 см.

2) Позначимо радіус циліндра - r. Тоді за умовою 2πr = 12π, звідси 2r = 12 (см). Тому АВ = 2r= 12 см.

Приклад 2. Відрізок, що сполучає центр верхньої основи циліндра з точкою кола нижньої основи дорівнює 4 см і утворює з площиною основи кут 45°. Знайти площу осьового перерізу циліндра.

Розв’язання. 1) Нехай O₁С - відрізок, що з’єднує центр верхньої основи - точку О₁ з точкою С кола нижньої основи (мал. 485). O₁С = 4 см.

2) ОС - проекція O₁С на площину нижньої основи, тому O₁CO - кут, що утворює відрізок O₁С з площиною нижньої основи. За умовою О₁СО = 45°.

4) АА₁В₁В - осьовий переріз, АА₁ = ОО₁ = 4 см; АВ = 2 ∙ АО = 4 ∙ 2 = 8 (см).

5) Тому площа діагонального перерізу S_AA1B1B = АВ ∙ АА₁ = 8 ∙ 4 = 32 (см²).

Переріз циліндра площиною, яка є паралельною до площини основ - круг, що дорівнює кругу основи циліндра (мал. 486). Радіус перерізу А₂O₂ дорівнює радіусу циліндра АО.

Перерізом циліндра площиною, паралельної осі циліндра є прямокутник. На малюнку 487 прямокутник АА₁В₁В - переріз циліндра площиною, паралельної осі циліндра ОО₁.

Дві його сторони: АА₁ і ВВ₁ - твірні циліндра, а дві інші: АВ і А₁В₁ - паралельні і рівні хорди основ.

Приклад 3. Паралельно осі циліндра проведено площину, яка відтинає від кола основи дугу 60º. Радіус основи циліндра дорівнює 6 см, а висота - 5 см. Знайти периметр отриманого перерізу.

Розв’язання. 1) Нехай АВВ₁А₁ - переріз, що задано в умові (мал. 487), АО = ОВ = 6 см, АА₁ = 5 см, AOB = 60°.

2) Оскільки АО = ОВ, то ∆АОВ - рівнобедрений,  Тому ∆АОВ - рівносторонній, АВ = ОА = 6 см.

3) Отже, периметр перерізу Р_ABB1B1B = 2(АА₁ + АВ) = 2(5 + б) = 22 (см).



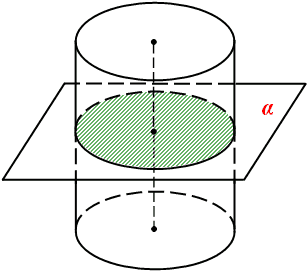
Теорема. Площина, паралельна площині основи циліндра, перетинає його бічну поверхню по колу, яке дорівнює колу основи.

Доведення. Нехай α - площина, паралельна площині основи циліндра. Паралельне перенесення вздовж напряму осі циліндра, яке суміщає площину α з площиною основи циліндра, суміщає переріз циліндричної поверхні (бічної поверхні) площиною α з колом основи. Теорему доведено.

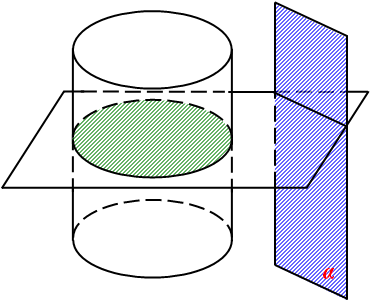	1)
2)
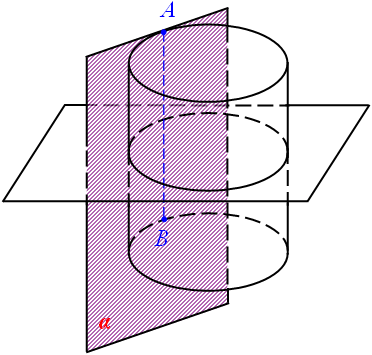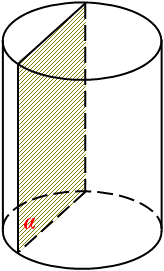	3)

Площина, яка паралельна осі циліндра, або не має з ним спільних точок (1), або дотикається циліндра (має з поверхнею одну спільну пряму АВ (2)), або перетинає циліндр (3), в перерізі маємо прямокутник. Означення. Переріз циліндра площиною, що проходить через його вісь, називається осьовим перерізом циліндра.

4)

   Означення. Циліндр називається рівностороннім, якщо його осьовий переріз є квадратом.

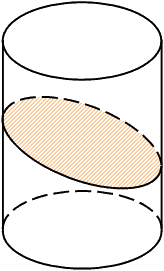
І нарешті, загальний випадок - площина не паралельна і не перпендикулярна осі циліндра. В цьому випадку вона перетинає циліндричну поверхню по деякій лінії. Ця лінія - еліпс - та чудова лінія, по якій рухаються планети та штучні супутники (4).

Дайте відповіді на питання:

1. Що таке круговий циліндр?
2. Дайте означення таким термінам: твірна циліндра, вісь циліндра, висота, радіус циліндра.
3. Який циліндр називається прямим?
4. Які перерізи циліндра ви знаєте?
5. Що таке осьовий переріз циліндра?
6. Який циліндр називається рівностороннім?