четвер, 23 квітня 2015 р.
середа, 22 квітня 2015 р.
Тест 1. Об’єми та поверхні тіл
Тест 7. Об’єми та поверхні тіл
Закінчити правильно
речення:
1.Об’єми двох кубів відносяться, як …
а) квадрати ребер; б)
довжини ребер; в) двогранні кути; г) куби ребер; д) інша відповідь.
2.Поверхні двох кубів відносяться, як …
А) квадрати ребер; Б)
довжини ребер; В) лінійні кути; Г) куби ребер; д) інша відповідь.
3.Об’єми двох правильних тетраедрів відносяться, як …
а) квадрати ребер; б)
довжини ребер; в) двогранні кути; г) куби ребер; д) інша відповідь.
4.Поверхні двох правильних тетраедрів відносяться, як
…
а) квадрати ребер; б)
довжини ребер; в) двогранні кути; г) куби ребер; д) інша відповідь.
5.Об'єми двох куль відносяться, як ...
а) квадрати радіусів; б)
довжини радіусів; в) довжини діаметрів; г) куби радіусів; д) інша відповідь.
6.Поверхні двох куль відносяться, як ...
а) квадрати радіусів; б)
довжини радіусів; в) довжини діаметрів; г) куби радіусів; д) інша відповідь.
7.Перерізом куба з площиною можуть бути …
а) будь-які n-кутники; б) будь-які
правильні n-кутники; в) будь-які гострокутні трикутники і чотирикутники; г) 5-кутники
і 6-кутники з паралельними сторонами; д) інша відповідь.
8.Перерізом правильного тетраедра з площиною можуть
бути …
а) будь-які n-кутники; б)
будь-які правильні n-кутники; в) будь-які гострокутні трикутники і
чотирикутники; г) 5-кутники і 6-кутники з не паралельними сторонами; д) інша
відповідь.
9.Перерізом сфери з площиною можуть бути …
а) будь-які еліпси; б)
будь-які кола; в) будь-які круги; г) параболи та гіперболи; д) інша відповідь.
10.Перерізом кулі з площиною можуть бути …
а) будь-які еліпси; б)
будь-які кола; в) будь-які круги; г) параболи та гіперболи; д) інша відповідь.
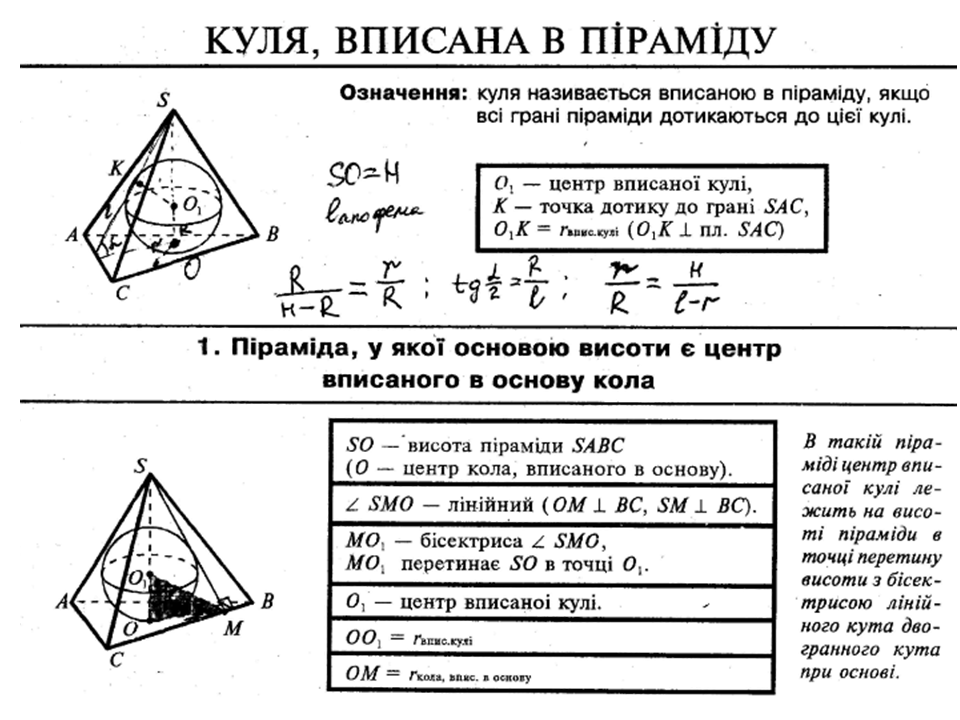
11.У трикутну піраміду можна вписати …
а) кулю; б) квадрат; в)
будь-які ромби; г) куб; д) інша відповідь.
12.Навколо трикутної піраміди можна описати …
а) кулю; б) паралелепіпед;
в) ромбоїд; г) куб; д) інша відповідь.
13.Навколо прямої трикутної призми можна описати …
а) сферу; б)
паралелепіпед; в) ромбоїд; г) куб; д) інша відповідь.
14.Умову прямої теореми про дотичну площину до кулі
записуємо так ...
а) радіус кулі є
перпендикуляром до дотичної площини; б) радіус кулі є похилою до дотичної
площини; в) радіус кулі є проекцією до дотичної площини; г) інша відповідь.
15.Точка М лежить на дотичній до кулі площині і віддалена
від центра на віддаль МО = 17, радіус кулі дорівнює 15. Відстань точки М від
точки дотику А дорівнює ...
а) 17; б) 15; в) 2; г)
інша відповідь.
16.У кулю вписано куб, а в куб кулю. Якщо через центр
кулі провести площину, перпендикулярно до ребра куба, то схематичний рисунок
перерізу має вигляд ...
а) квадрат описаний і
вписаний; б) трикутник описаний і вписаний; в) чотирикутник описаний і
вписаний; г) інша відповідь.
17.Центр кулі, вписаної в правильну трикутну призму, лежить на
...
а) прямій, що є віссю симетрії основи призми; б)
будь-якому трикутнику, що паралельний основам; в) перетині діагоналей вписаного
в кулю чотирикутника; д) інша відповідь.
18.Якщо радіус
кулі дорівнює r, то висота призми дорівнює …
а) r; б) 0,5r; в) 2r; г) 1,5r; д) інша відповідь.
19.Висота трикутника,
який лежить в основі правильного тетраедра з ребром а, дорівнює ...
а) 30,5а; б) 30,5а/2; в) 2а; г) 1,5а/4; д) інша відповідь.
20.Висота правильної
трикутної призми з усіма рівними ребрами а дорівнює ...
а) 30,5а; б) 30,5а/2; в) 2а; г) 1,5а/4; д) інша відповідь.
21.Висота правильної
трикутної піраміди з усіма
рівними ребрами а дорівнює ...
а) 30,5а; б) 30,5а/2; в) 2а; г) 1,5а/4; д) інша відповідь.
22.Площа основи
правильної трикутної призми з усіма
рівними ребрами а дорівнює ...
а) 30,5а2; б) 30,5а2/4; в) 2а2/3;
г) 1,5а2/4; д) інша відповідь.
23.Об'єм правильної трикутної призми з усіма рівними ребрами а дорівнює ...
а) 30,5а3; б) 30,5а3/4; в) 2а3/3;
г) 1,5а3/4; д) інша відповідь.
24.Об'єм правильної трикутної піраміди з
усі рівними ребрами а дорівнює ...
а) 30,5а3; б) 30,5а3/4; в) 2а3/3;
г) 1,5а3/4; д) інша відповідь.
25.Півкруг радіуса R згорнуто в конус, об'єм якого буде дорівнювати ...
а) 30,5R3p; б) 30,5pR3/4; в) 2pR3/3; г) 1,5pR3/4; д) інша відповідь.
26.Геометричним
місцем точок простору, рівновіддаленних від однієї точки, є ...
а) куля; б) куб; в) двогранні кути; г) відрізок; д)
інша відповідь.
27.Об'єм кулі дорівнює . ..
а) 30,5R3p; б) 30,5pR3/4; в) 2pR3/3; г) 4pR3/3; д) інша відповідь.
28.Поверхня кулі дорівнює . ..
а) 4R2p; б) 30,5pR2/4; в) 2pR2/3; г) 4pR2/3; д) інша відповідь.
29.Бічна поверхня конуса дорівнює
. ..
а) lRp; б) plR2/4; в) 2lpR2/3; г) 4lpR2/3; д) інша відповідь.
30.Об'єм конуса дорівнює . ..
а) 30,5R2pН; б) 30,5pR2Н/3; в) 2pНR2/3; г) pНR2/3; д) інша відповідь.
31.Поверхня конуса дорівнює . ..
а) 4R2p; б) 30,5pR2/4; в) 2pR2/3; г) 4pR2/3; д) інша відповідь.
32.Бічна поверхня циліндра дорівнює . ..
а) НRp; б) pНR2/4; в) 2НpR2/3; г) 4НpR2/3; д) інша відповідь.
33.Радіус кулі,
вписаної в правильний тетраедр з ребром а, дорівнює ...
а) 30,5а; б) 30,5а/4; в) 2а/3;
г) 1,5а/4; д) інша
відповідь.
34.Радіус кулі, описаної навколо правильного тетраедра з ребром а, дорівнює ...
а) 30,5а; б) 30,5а/4; в) 2а/3;
г) 1,5а/4; д) інша
відповідь.
33.Радіус кулі,
вписаної в куб з ребром а, дорівнює ...
а) 30,5а; б) 30,5а/4; в) 2а/3;
г) 1,5а/4; д) інша
відповідь.
34.Радіус кулі, описаної навколо куба з ребром а, дорівнює ...
а) 30,5а/2; б) 30,5а/4; в) 2а/3;
г) 1,5а/4; д) інша
відповідь.
Задачі на призмах
1. Основою прямокутної призми є прямокутний трикутник із
катетом 5 см і гіпотенузою 13 см. Висота призми дорівнює 8 см. Знайдіть
поверхню бічної поверхні призми.
2.
Знайдіть
площу діагонального перерізу прямокутного паралелепіпеда, якщо його висота
дорівнює 12 см, а сторони основи - 8 см і 6 см.
3. Двогранний кут
дорівнює 30о. Точка А, що
лежить на одній із граней цього кута, віддалена, від ребра цього кута на 12 см.
Знайдіть відстань від точки А до
другої грані.
Розв’язання
до завдань 10-12 повинно містити креслення й повне пояснення, записане у
вигляді послідовних логічних дій, із посиланням на математичні факти, з яких
випливає те чи інше твердження. Одержану відповідь перенесіть у бланк відповідей.
10. Основою
піраміди є прямокутний трикутник із гострим кутом a і гіпотенузою c.
Дві бічні грані, що містять сторони цього кута, перпендикулярні до площини
основи, а третя – нахилена до площини основи під кутом β. Знайдіть об’єм
піраміди. Обчисліть, якщо с = 4 см, α
= 30о, β = 45о.
11. Основа прямого
паралелепіпеда – ромб із більшою діагоналлю 4(3)0,5 см і гострим
кутом 60о. Знайдіть повну поверхню паралелепіпеда Sповн. У відповідь запишіть Sповн.:(3)0,5.
12. Сторони трикутника дорівнюють 13 см, 14 см і 15 см. Знайдіть
відстань від площини трикутника до центра кулі, яка дотикається до всіх його
сторін, якщо радіус кулі дорівнює (5)0,5 см.
Задачі на комбінації тіл у просторі
Задачі для геометричного тренінгу
КОМБІНАЦІЯ
КОНУСА І КУЛІ
1. а)
Навколо конуса, осьовим перерізом
якого є гострокутний рівнобедрений
трикутник, описано кулю радіуса R. Радіус кулі, проведений до точки кола основи
конуса, утворює з площиною цієї основи кут w. Визначити об'єм конуса.
б)
Навколо конуса описано кулю. Твірна конуса утворює з площиною
основи кут w. Висота конуса дорівнює H. Знайти об'єм кулі.
2. а) У
конус вписано кулю радіуса r. Твірна конуса нахилена до площини основи під кутом w. Визначити об'єм конуса.
б)
У конус вписано кулю. Твірна конуса нахилена до площини основи під кутом w. Висота конуса дорівнює H. Визначити об'єм кулі.
1. а ) Основою піраміди
є рівнобедрений трикутник з основою а і кутом w при
вершині. Усі бічні ребра піраміди утворюють з площиною основи кут v. Визначити бічну поверхню конуса, описаного навколо даної піраміди.
б)
Основою піраміди є рівнобедрений трикутник з бічною стороною
b і кутом w при
основі. Усі двогранні кути при основі піраміди дорівнюють v. Визначити бічну поверхню конуса, вписаного в дану піраміду.
2. а)
Основою піраміди є прямокутний трикутник з катетом а
і прилеглим до нього гострим кутом w. Усі бічні ребра піраміди утворюють з площиною
основи кут v. Визначити об'єм конуса,
описаного навколо даної піраміди.
б)
Основою піраміди є прямокутний трикутник з гіпотенузою с
і гострим кутом w. Усі
двогранні куги при основі піраміди дорівнюють v. Визначити об'єм конуса,
вписаного в дану піраміду.
3. а) В
основі піраміди лежить гострокутний трикутник. Усі бічні ребра піраміди утворюють з площиною основи кут a. Відстань від основи висоти
піраміди до однієї із сторін основи дорівнює d, а кути, прилеглі до цієї сторони, дорівнюють w і v. Визначити бічну поверхню конуса, описаного навколо даної піраміди.
б)
У трикутній піраміді всі двогранні
кути при основі дорівнюють a.
Відстань від основи висоти піраміди до вершини одного із кутів основи дорівнює d, а два інші кути основи дорівнюють w і v.
Визначити бічну поверхню конуса,
вписаного в дану піраміду.
4. а) В
основі піраміди лежить прямокутник, діагональ якого утворює з більшою стороною кут а. Усі бічні ребра піраміди нахилені до площини основи під кутом w.
Відрізок, що сполучає середину більшої сторони прямокутника з
основою висоти піраміди, дорівнює d.
Визначити об'єм конуса, описаного
навколо даної піраміди.
б)
В основі піраміди лежить ромб з гострим кутом а.
Усі двогранні кути при основі піраміди дорівнюють w. Відрізок, що сполучає основу висоти піраміди з
серединою сторони ромба, дорівнює b.
Визначити об'єм конуса, вписаного в
дану піраміду.
5. а) Основою піраміди є рівнобічна трапеція з гострим кутом а. Діагональ трапеції перпендикулярна до бічної
сторони. Усі бічні ребра піраміди утворюють з її висотою кут w. Відстань від основи висоти піраміди до бічної
сторони трапеції дорівнює b.
Визначити бічну поверхню конуса,
описаного навколо даної піраміди.
б)
У піраміду, основою якої є рівнобічна трапеція з тупим кутом w, вписано конус. Усі двогранні кути при основі
піраміди дорівнюють v.
Відстань від основи висоти піраміди до вершини даного кута трапеції дорівнює а.
Визначити бічну поверхню конуса.
КОМБІНАЦІЯ
ПІРАМІДИ І КУЛІ
1. а) Навколо правильної чотирикутної піраміди
описано кулю. Бічне ребро піраміди
утворює з площиною основи кут w.
Висота піраміди дорівнює H.
Визначити об'єм кулі.
б)
Навколо правильної трикутної піраміди
описано кулю. Висота піраміди
дорівнює H і утворює з бічним ребром кут у. Визначити об'єм кулі.
2. а) Навколо правильної
чотирикутної піраміди описано кулю
радіуса R. Бічне ребро піраміди утворює з площиною основи кут w. Визначити
об'єм піраміди.
б)
Навколо правильної трикутної піраміди
описано кулю радіуса R. Бічне ребро піраміди утворює з площиною основи кут w. Визначити об'єм піраміди.
3. а) В основі піраміди лежить рівнобедрений трикутник з кутом w при вершині. Усі бічні ребра піраміди нахилені до
площини основи під кутом v.
Визначити об'єм піраміди, якщо
радіус описаної навколо неї кулі
дорівнює R.
б)
В основі піраміди лежить прямокутний трикутник з гострим кутом а.
Усі бічні ребра піраміди нахилені до площини основи під кутом v. Визначити об'єм піраміди,
якщо радіус описаної навколо неї кулі
дорівнює R.
4. а) У правильну трикутну піраміду вписано кулю радіуса r. Бічна грань піраміди нахилена до площини основи під
кутом w. Визначити об'єм
піраміди.
б)
У правильну трикутну піраміду
вписано кулю. Бічна грань піраміди
нахилена до площини основи під кутом а. Висота піраміди дорівнює H. Визначити об'єм кулі.
5. а) У правильну чотирикутну піраміду вписано кулю радіуса R. Двогранний кут при основі піраміди дорівнює а.
Визначити повну поверхню піраміди.
б)
У правильну чотирикутну піраміду
вписано сферу. Двогранний кут при
основі піраміди дорівнює w.
Висота піраміди дорівнює H. Визначити
поверхню сфери.
6. а)
В основі піраміди лежить рівнобедрений трикутник з кутом а
при основі. Усі двогранні кути при основі піраміди дорівнюють w. Визначити об'єм піраміди,
якщо радіус вписаної кулі дорівнює r.
б)
В основі піраміди лежить прямокутний трикутник з гострим кутом а.
Усі двогранні кути при основі піраміди дорівнюють w. Визначити об'єм піраміди, якщо радіус вписаної кулі дорівнює r.
КОМБІНАЦІЯ
ПРИЗМИ І СФЕРИ
1. а) Навколо правильної
чотирикутної призми описано сферу. Радіус сфери, проведений до вершини призми, утворює з її бічним ребром кут w.
Визначити поверхню сфери, якщо бічне
ребро призми дорівнює а.
б)
Навколо правильної трикутної призми
описано кулю. Радіус кулі,
проведений до вершини призми, утворює з її бічним ребром кут w. Визначити об'єм кулі,
якщо бічне ребро призми дорівнює b.
2. а) Навколо правильної
чотирикутної призми описано кулю радіуса R.
Радіус кулі, проведений до вершини призми, утворює з площиною її основи кут w.
Визначити бічну поверхню призми.
б)
Навколо правильної трикутної призми описано кулю радіуса R. Радіус кулі, проведений до вершини призми, утворює з площиною її основи кут w. Визначити
об'єм призми.
КОМБІНАЦІЯ
ПРИЗМИ І ЦИЛІНДРА
1. а)
Основою прямої призми є рівнобедрений трикутник з кутом w при вершині. Діагональ бічної грані, що містить
основу цього трикутника, дорівнює d і нахилена до площини основи під кутом а. Визначити бічну
поверхню циліндра, описаного навколо
призми.
б)
Основою прямої призми є рівнобедрений трикутник з кутом а
при основі. Діагональ бічної грані, що містить бічну сторону цього трикутника,
дорівнює b і нахилена до площини основи під кутом w. Визначити бічну поверхню циліндра, вписаного в дану призму.
2. а) Основою призми є трикутник зі
стороною с та прилеглими до неї кутами v і w.
Діагональ бічної грані, що містить цю сторону трикутника, нахилена до площини
основи під кутом a.
Визначити об'єм циліндра, описаного
навколо даної призми.
б)
Основою прямої призми є прямокутний трикутник з гострим кутом a. Діагональ бічної грані, що містить прилеглий до
цього кута катет, дорівнює d і нахилеиа до площини основи під кутом w. Визначити об'єм циліндра, описаного навколо даної призми.
3. а) Основою прямої призми є прямокутний
трикутник з гострим кутом а. Діагональ бічної грані, що
містить гіпотенузу, дорівнює d і
нахилена до площини основи під кутом w. Визначити об'єм циліндра,
вписаного в дану призму.
б)
Основою прямої призми є трикутник з кутами w і v.
Діагональ бічної грані, що містить сторону, для якої дані кути є прилеглими,
дорівнює d і нахилена до площини основи під кутом a. Визначити об'єм циліндра,
вписаного в дану призму.
4. а) В основі прямої призми лежить прямокутник,
діагональ якого утворює з більшою стороною кут w. Діагональ бічної грані призми, що
містить меншу сторону прямокутника, дорівнює d і утворює з площиною основи кут а. Визначити бічну
поверхню циліндра, описаного навколо даної призми.
б)
Основою прямої призми є ромб з гострим кутом а.
Діагональ бічної гранг призми дорівнює d і утворює з площиною основи кут w. Визначити бічну поверхню циліндра, вписаного в дану призму.
5. а) Основою прямої призми є рівнобічна трапеція з гострим кутом а.
Діагональ трапеції є бісектрисою гострого кута. Діагональ бічної грані, що містить бічну сторону трапеції, дорівнює d і утворює з площиною основи
кут w. Визначити об'єм циліндра,
описаного навколо даної призми.
б)
У пряму призму, основою якої є рівнобічна трапеція з тупим кутом w, вписано циліндр.
Діагональ бічної грані, що містить бічну сторону трапеції, дорівнює а
і нахилена до площини основи під кутом w. Визначити об'єм циліндра.




вівторок, 21 квітня 2015 р.
Підписатися на:
Коментарі (Atom)